포함-배제의 원리 소개

아래에 있는 그림에 관한 이야기로 이야기를 시작해보자. 원소를 \(t\)개 갖고 있는 어떤 전체집합이 있고 그 전체집합의 세 부분집합 \(A, B, C\)가 있을 때, 원소의 개수와 관련된 성질을 관찰해보자. 그림의 직사각형은 전체집합을 나타낸다. 각각의 집합 \(S\)에 대하여, \(S\)의 원소의 개수를 \(\vert S\vert\)로 나타내며 이를 집합 \(S\)의 크기(size)라고 말한다. 그림에 있는 세 개의 다이어그램에서 첫 번째를 보면 자명하면서도 매우 중요한 성질을 찾을 수 있다. 우리가 이미 알고 있듯이 어떤 집합의 원소를 셀 때 거꾸로 세는 것, 즉 그 집합에 속하지 않은 원소의 개수를 세는 것이 유용할 때가 많이 있다. 예를 들어 모음이 들어 있는 \(5\)-letter word의 개수를 직접 세는 것은 꽤 번거롭지만, 거꾸로 생각하여, 모음이 없는 \(5\)-letter word의 개수를 먼저 세어 \(26^{5}-21^{5}\)라는 답을 쉽게 구할 수 있다.

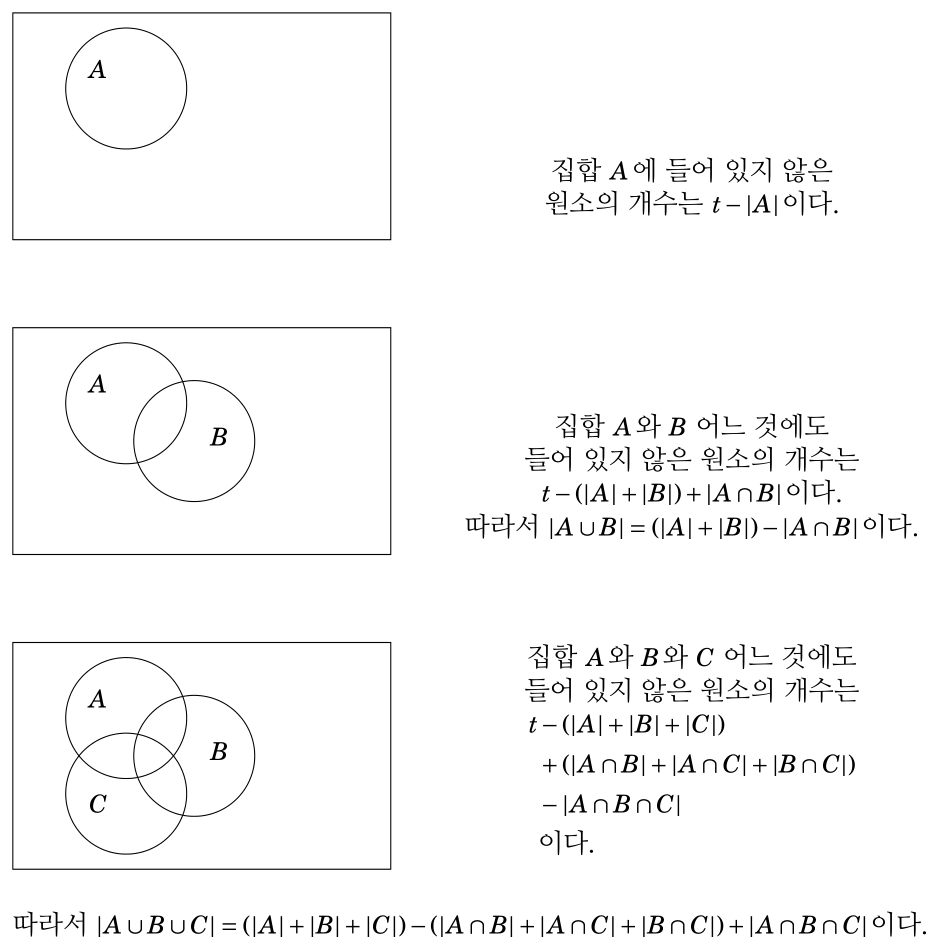
그림의 두 번째 내용은 간단히 증명할 수 있는 상식이라 할 수 있지만 그림의 세 번째 부분은 약간의 설명이 필요할 수 있다. 세 집합 \(A, B, C\) 어디에도 들어 있지 않은 원소의 개수를 세기 위해, 먼저 다이어그램에 표시된 \(8\)개의 영역 각각에 \(+1\)을 한 번씩 쓰자. 그리고 \(A\)에 포함된 \(4\)개의 영역 각각에 \(-1\)을 한 번씩, \(B\)에 포함된 \(4\)개의 영역 각각에도 \(-1\)을 한 번씩, \(C\)에 포함된 \(4\)개의 영역 각각에도 \(-1\)을 한 번씩 쓰자. 다음으로 \(A, B, C\) 중 적어도 두 개의 집합에 포함된 영역 각각에 또 \(+1\)을 한 번씩 쓴 후, 마지막으로 \(A, B, C\) 모두에 포함된 영역에 \(-1\)을 한 번 쓴다. 그러면 \(A, B, C\) 어디에도 속하지 않는 원소들이 있는 영역에 써있는 수의 합은 \(+1\), 나머지 \(7\)개의 각 영역에는 써진 수의 합이 \(0\)이 되도록 수가 써있게 된다.

이제 소위 포함-배제의 원리(the principle of inclusion and exclusion¹)라고 부르는 것을 이해할 수 있을 것이다. 위의 절차를 잘 살펴보면, 예를 들어 \(A\cap B\cap C\)의 원소는 \(t\)에서 한 번 포함되고, \(\vert A\vert+\vert B\vert +\vert C\vert\)에서 \(3\)번 배제되며, \(\vert A\cap B\vert +\vert B\cap C\vert +\vert C\cap A\vert\)에서 \(3\)번 포함되며, 마지막으로 \(\vert A\cap B\cap C\vert\)에서 한 번 배제되어 총 \(0\)번 세어짐을 확인할 수 있다. 이는 조금은 지루해보이기도 하지만 굉장히 강력한 원리를 보여준다. 독자는 아마 일반적인 패턴을 추측할 수 있을 것이다. 일반화된 패턴의 증명은 다음 절에서 하기로 하고 여기서는 기본적인 다음 문제를 해결해보자. 이 문제들은 모두 위의 그림에 기술된 결과를 기반으로 해결할 수 있는 문제들이다.

PIE Problems I.

1. 아홉자리로 구성된 사회보장번호 체계가 있다고하자. 각 자리에는 \(0\)에서 \(9\)까지의 수가 하나 있다고
할 때, 반복된 자릿수가 있는 사회보장번호의 개수는?
2. 첫 글자 혹은 마지막 글자가 모음인 \(4\)-letter word는 몇 개인가?
3. 첫 글자와 마지막 글자 중 어느 것도 모음이 아닌 \(4\)-letter word는 몇 개인가?
4. 서로 구별되는 \(3\)개의 상자에 \(25\)개의 빨간색 공을 담을 때, \(15\)개 보다 많은 공이 담긴 상자가
없도록 공을 담는 경우의 수는?
5. 서로 구별되는 \(3\)개의 상자에 \(25\)개의 빨간색 공을 담을 때, \(10\)개 보다 많은 공이 담긴 상자가
없도록 공을 담는 경우의 수는?
6. COMBINATORICS의 글자들을 배열할 때, 두 개의 C가 모두 두 개의 I 보다 왼쪽에 있거나 두 개의 O가
모두 두 개의 I 보다 왼쪽에 있도록 배열하는 경우의 수는?
7. 방정식 \(x_{1}+x_{2}+x_{3}=18\)의 정수해 중, \(0\leq x_{i}\leq 9\ (i=1, 2, 3)\)을 만족시키는 해의 개수는?
8. \(0\)부터 \(9\)까지의 \(10\)개의 숫자로 만든 순열 중 수열 \(024\) 혹은 수열 \(456\)을 포함하는 순열의
개수는?
9. \(0\)부터 \(9\)까지의 \(10\)개의 숫자로 만든 순열 중 세 수열 \(123, 345, 567\) 중 적어도 하나를
포함하는 순열의 개수는?
10. 한 주사위를 \(7\)번 던질 때, 다섯 번째 던져 나온 눈이 그보다 먼저 던져서 나온 눈과 일치하는 경우의
수는?

1. 앞으로 이를 종종 PIE로 간단히 나타낼 것이다.