제3장 문자와 식
3.1 다항식
다항식의 구조1
문자 또는 수들의 곱으로 이루어진 식을 항이라 하고, 항 또는 항들의 합으로 이루어진 식을 다항식(polynomial)이라고 한다.2 예를 들어 \[ \pi,\quad x,\quad 3z+1,\quad -x+2x^{2020}+2, \quad -xy^{2}+x^{2}+a^{4}y^{2}+x \] 는 모두 다항식이다.3 4
다항식은 동류항끼리 모아서 정리하여 간단히 나타낸다. 그리고 차수가 높은 항부터 순서대로 나열하는 내림차순 혹은 차수가 낮은 항부터 순서대로 나열하는 오름차순으로 정리하면 보기 좋다.5 예를 들어 다항식 \(-x+2x^{2020}+2\)를 내림차순과 오름차순으로 정리하면 다음과 같다. \[ 2x^{2020}-x+2,\quad 2-x+2x^{2020} \] 문자가 두 개 이상있는 다항식은 하나의 문자를 기준으로 정리한다. 이때 기준으로 삼는 문제를 제외한 다른 문자는 모두 상수로 생각한다. 예를 들어 다항식 \(-xy+x^{2}+a^{3}y^{2}+x\)를 \(x\)를 기준으로 내림차순으로 정리하면 \[ x^{2}+(-y+1)x+a^{3}y^{2} \] 이며 이를 다시 \(y\)에 관한 오름차순으로 정리하면 \[ x^{2}+x-xy+a^{3}y^{2} \] 이다.
보기 다항식 \(x^2+2xy^{2}+7y-3\)을 문자 \(x\)에 대하여 생각했을 때는 \(2xy^{2}\)는 \(1\)차항이며 \(1\)차항의 계수는 \(2y^{2}\)이다. 그러나 별다른 언급 없이 이 다항식이 몇 차 다항식인가 물었을 때는 (\(x, y\)에 대한) \(3\)차식이라고 답하는 것이 좋다.
다항식의 덧셈은 식을 눈치껏 잘 정리해서6 동류항끼리 계산하면 된다. 다항식의 뺄셈은 빼는 다항식의 각 항의 부호를 바꾸어 더하여 계산한다. 물론 지금 다루고 있는 문자는 실수 혹은 복소수를 대신하여 나타낸 것이니 결합법칙과 분배법칙과 같은7 연산에 관한 좋은 성질들을 적절히 이용하여 계산할 수 있다.
예를 들어, 두 다항식 \(2x^{2}+x+1\)과 \(5-3x-x^{2}+3x^{3}\)의 덧셈은 \begin{align*} (2x^{2}+x+1) + (5-3x-x^{2}+3x^{3}) & = 2x^{2}+x+1 + 5-3x-x^{2}+3x^{3} \\ & = 3x^{3} +(2-1)x^{2}+(1-3)x + (1+5) \\ & = 3x^{3}+x^{2}-2x+6 \end{align*} 으로, 뺄셈은 \begin{align*} (2x^{2}+x+1) - (5-3x-x^{2}+3x^{3}) & = (2x^{2}+x+1) +( -5+3x+x^{2}-3x^{3}) \\ &= 2x^{2}+x+1 -5+3x+x^{2}-3x^{3} \\ & = - 3x^{3} +(2+1)x^{2}+(1+3)x + (1-5) \\ & = -3x^{3}+3x^{2}+4x-4 \end{align*} 로 계산할 수 있다. 물론 이 계산을 다음과 같이 동류항을 맞추어 세로셈으로 할 수도 있다.8

유제 3.1 주어진 두 다항식 \(A, B\)에 대하여 \(A+B\)와 \(A-B\)를 각각 구하여라.
- \(A=3a^{3}-2a-1,\quad B=7a^{3}-3a^{2}+2a+4\)
- \(A=x^{2}+2xy+5y^{2},\quad B=2x^{2}-4xy+2y^{2}\)
유제 3.1의 결과를 보고 잠시 생각해보면 다항식 전체의 집합은 덧셈에 대하여 닫혀 있음을 알 수 있다. 그리고 다항식의 덧셈에 있어서도 덧셈에 대한 결합법칙 및 교환법칙이 성립함을 알 수 있다. 또한 \(A\)가 임의의 다항식일 때, \(A+0=0+A=A\)이므로 다항식 \(0\)은 다항식의 덧셈에 대한 항등원이다. 그리고 다항식 \(A\)의 덧셈에 대한 역원이 \(-A\)인 것도 바로 알 수 있다. 다항식의 덧셈에 관한 기본 성질을 정리하면 다음과 같다.9
Proposition 3.1.1 (다항식의 덧셈에 대한 기본 성질)
- 임의의 다항식 \(A, B, C\)에 대하여 (결합법칙)
\(\phantom{임의의 다항식}\) \((A+B)+C=A+(B+C)\) - 임의의 다항식 \(A, B\)에 대하여 \(A+B=B+A\) (교환법칙)
- 덧셈에 대한 항등원 \(0\)이 있다. (항등원)
- 임의의 다항식 \(A\)는 덧셈에 대한 역원 \(-A\)를 갖는다. (역원)
이제 다항식의 곱셈을 살펴보자. 다항식의 곱셈은 다항식을 전개하는 것과 같다. 두 다항식의 곱셈에서도 식을 눈치껏 잘 정리해서 결합법칙, 교환법칙 그리고 곱셈의 덧셈에 대한 분배법칙을 잘 활용하여 계산하면 된다. 다음 예제로 설명을 대신한다.
예제 3.2 다음 식을 전개하여라.
- \((2x^{2}+3x-1)(x+5)\)
- \((x+3y-1)(x-2y)\)
Sol.
- \begin{align*} (2x^{2}+3x-1)(x+5)&=2x^{2}(x+5)+3x(x+5)-(x+5) \\ &=2x^{3}+10x^{2}+3x^{2}+15x-x-5 \\ &= 2x^{3}+13x^{2}+14x-5 \end{align*}
- \begin{align*} (x+3y-1)(x-2y) & = x(x-2y)+3y(x-2y)-(x-2y) \\ & = x^{2}-2xy+3xy -6y^{2}-x +2y \\ & = x^{2}+xy-6y^{2} -x +2y \end{align*}
유제 3.3 위의 예제 3.2의 풀이에서 각 줄의 등호에 사용한 성질이 무엇인지 설명하여라.
유제 3.4 다음 식을 전개하여라.
- \((a^{2}-2a-1)(a^{2}+4)\)
- \((x+2y-2)(x-y-3)\)
다항식의 곱셈은 분배법칙을 이용하여 전개할 수도 있지만 특별한 모양의 곱셈은 중학교에서 배운 다음 곱셈 공식들을 이용하면 편리하다. \begin{align*} (a+b)^{2} & =a^{2} +2ab+b^{2} \\ (a-b)^{2} & =a^{2} -2ab+b^{2} \\ (a+b)(a-b) &=a^{2} -b^{2} \\ (x+a)(x+b) & =x^{2} +(a+b)x+ab \\ (ax+b)(cx+d) & =acx^{2} +(ad+bc)x+bd \end{align*}
위 공식을 이용하여 좀 더 복잡한 식을 전개하여 보자. 예를 들어, 곱셈 공식 \((a+b)^{2} =a^{2} +2ab+b^{2}\)을 이용하여 \((a+b+c)^{2}\)과 \((a+b)^{3}\)을 전개하면 다음과 같다. \begin{align*} (a+b+c)^{2} & = \left( (a+b)+c\right)^{2} \\ & =(a+b)^{2} +2(a+b)c+c^{2} \\ & =a^{2} +2ab+b^{2} +2ac+2bc+c^{2} \\ & =a^{2} +b^{2} +c^{2} +2ab+2bc+2ca, \\ (a+b)^{3} & =(a+b)^{2} (a+b) \\ & =(a^{2} +2ab+b^{2} )(a+b) \\ & =a^{3} +a^{2} b+2a^{2} b+2ab^{2} +ab^{2} +b^{3} \\ & =a^{3} +3a^{2} b+3ab^{2} +b^{3} \end{align*} 한편, 위 등식에서 \(b\) 대신 \(-b\)를 대입하면 \[ (a-b)^{3} =a^{3} -3a^{2} b+3ab^{2} -b^{3} \] 이다.
유제 3.5 다음 등식이 성립함을 보여라.
- \((a+b)\left(a^2-ab+b^{2}\right)=a^{3}+b^{3}\)
- \((a-b)\left(a^{2}+ab+b^{2}\right)=a^{3}-b^{3}\)
이로부터 다음과 같은 공식을 얻는다.10
Theorem 3.1.2 (곱셈 공식)
- \((a+b+c)^2 =a^2 +b^2 +c^2 +2ab +2bc +2ca \)
- \((a+b)^3 =a^3 +3a^2 b +3ab^2 +b^3,\)
\((a-b)^3=a^3 -3a^2 b +3ab^2 -b^3\) - \((a+b)(a^2 -ab +b^2) =a^3 +b^3,\)
\((a-b)(a^2 +ab +b^2 ) =a^3 -b^3\)
예제 3.6 곱셈 공식을 이용하여 다음 식을 전개하여라.
- \((a+b-c)^{2}\)
- \((x+2)^{3}\)
Sol.
- \begin{align*} (a+b-c)^{2}&=a^{2} +b^{2} +(-c)^{2} +2\cdot a\cdot b \\ &\phantom{MMMMMMMM} +2\cdot b \cdot (-c) +2\cdot (-c)\cdot a \\ & =a^{2} +b^{2} +c^{2} +2ab-2bc-2ca \end{align*}
- \begin{align*} (x+2)^{3} & =x^{3} +3\cdot x^{2} \cdot 2+3\cdot x\cdot 2^{2} +2^{3}\\ & =x^{3} +6x^{2} +12x+8 \end{align*}
유제 3.7 곱셈 공식을 이용하여 다음 식을 전개하여라.
- \((2x-y+3)^{2}\)
- \((2a-3)^{3} \)
- \((x+2)(x^{2} -2x+4)\)
- \((x-3y)(x^{2} +3xy+9y^{2} )\)
지금까지의 계산에서 알 수 있듯이 두 다항식의 곱셈의 결과는 항상 다항식이므로 다항식 전체의 집합은 곱셈에 대하여 닫혀 있다. 그리고 다항식에서도 실수와 마찬가지로 곱셈에 대하여 교환법칙과 결합법칙이 성립하며, 곱셈의 덧셈에 대한 분배법칙이 성립한다. 또한 \(1\)은 곱셈에 대한 항등원이다.
Theorem 3.1.3 (다항식의 곱셈에 대한 기본 성질)
- 임의의 다항식 \(A, B\)에 대하여 \(AB=BA\) (교환법칙)
- 임의의 다항식 \(A, B, C\)에 대하여 \((AB)C=A(BC)\) (결합법칙)
- 임의의 다항식 \(A, B, C\)에 대하여 (분배법칙11)
\(\phantom{임의의 다항식}\) \(A(B+C)=AB+AC\) - 곱셈에 대한 항등원 \(1\)이 있다. (항등원)
유제 3.8 다항식 전체의 집합에 있는 원소 중 곱셈에 대한 역원을 갖는 원소는 무엇인지 설명하여라.
유제 3.8에서 알 수 있듯이 다항식 전체의 집합에서의 곱셈에서는 곱셈에 대한 역원을 갖지 않는 원소가 대부분이라 할 수 있다. 이는 다항식 전체의 집합에서의 나눗셈을 유리수, 실수, 복소수의 경우에서처럼 할 수는 없음을 뜻한다. 그러나 다항식의 나눗셈을 정수의 나눗셈에서처럼 몫과 나머지를 구하는 과정으로 생각할 수 있다. 즉 주어진 다항식을 \(0\)이 아닌 다항식으로 나눌 때, 각 다항식을 내림차순으로 정리하여 정수의 나눗셈과 같은 방법으로 계산한다.
예를 들어 \((2x^{2}+5x-5)\div (x+3)\)은 다음과 같이 계산한다.

위의 계산에서, 정수의 나눗셈에서 그랬던 것처럼, \(2x-1\)을 몫이라 부르고 \(-2\)을 나머지라 부르면 그럴듯 하다.12 그리고 정수의 나눗셈에서처럼 나눗셈의 결과를 \[ 2x^{2} +5x-5=(x+3)(2x-1)-2 \] 와 같이 나타낼 수 있다.
일반적으로 다항식의 나눗셈에서 다음이 성립한다.
Theorem 3.1.4 (다항식의 나눗셈에 대한 성질: 유클리드 알고리즘)
다항식 \(A\)와 \(0\)이 아닌 다항식 \(B\)에 대하여
\[
A=BQ+R,\quad \mbox{단, \(\deg(R) < \deg(B)\)}
\]
인 다항식 \(Q, R\)이 존재한다. [efn_note] 다항식 \(A\)의 차수를 \(\deg(A)\)로 나타낸다.[/efn_note]
특히, \(R=0\)이면 \(A=BQ\)이다. 이 경우 정수와 마찬가지로 \(A\)는 \(B\)로 나누어 떨어진다고 말한다.
유제 3.9 다음 나눗셈의 몫과 나머지를 구하고, 그 결과를 \(A=BQ+R\) 꼴로 나타내어라.
- \((2x^{2} +5x-2)\div (2x+1)\)
- \((3x^{3} +5x+2)\div (x^{2} -1)\)
- \((x^{3} -3x^{2} -6x+8)\div (x-2)\)
- \((x^{3} -3x^{2} +x-1)\div (x^{2} -2x-3)\)
다항식을 \(x-a\)와 같은 일차식으로 나눌 때에는 직접 나누지 않고 계수만을 이용하여 몫과 나머지를 구하는 방법이 있다. 예를 들어, \(3x^{3} -3x^{2} +2x+4\)를 \(x-2\)로 직접 나누면 다음과 같다.13
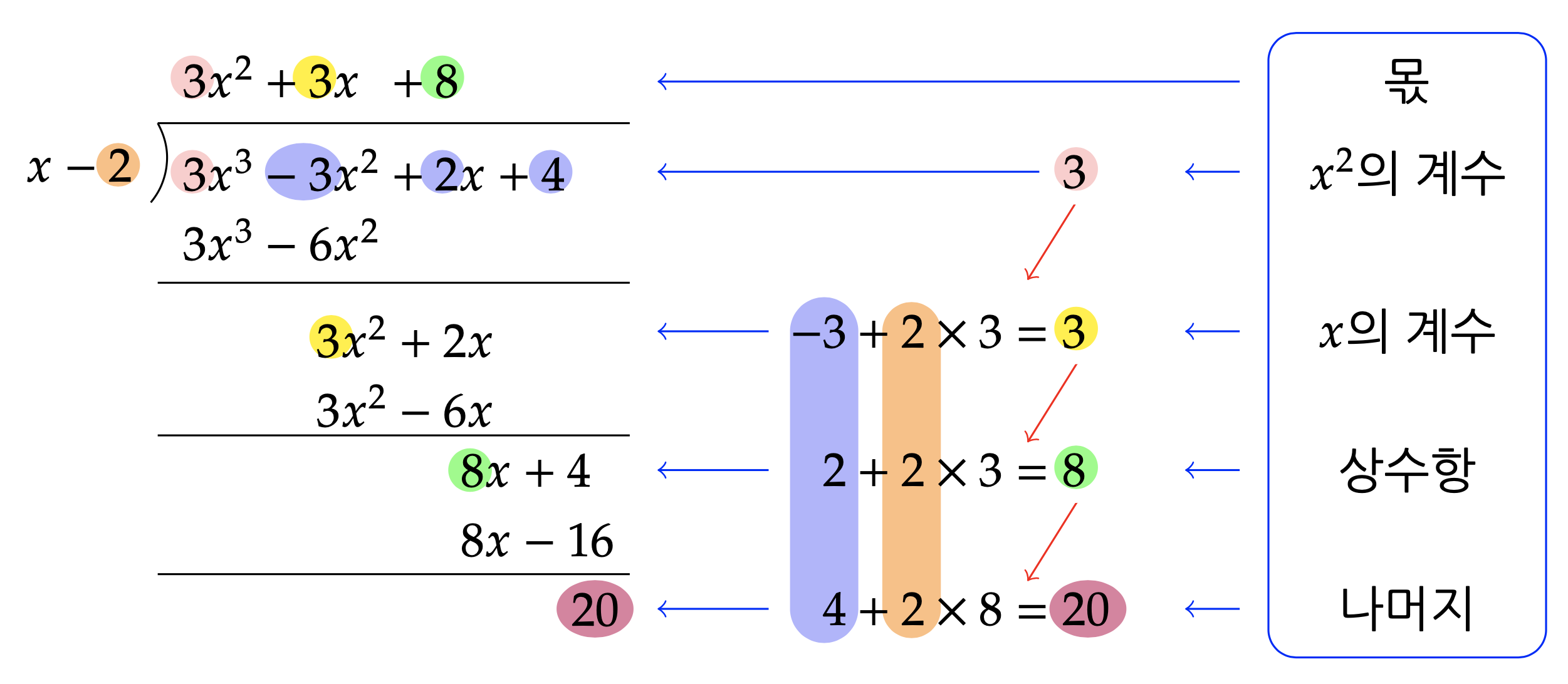
따라서 \(3x^{3} -3x^{2} +2x+4\)를 \(x-2\)로 나누었을 때 몫은 \(3x^{2} +3x+8\)이고 나머지는 \(20\)이다. 이때, 위 계산 과정에서 계수만 생각하여 다음과 같은 방법 으로 몫과 나머지를 간단히 구할 수 있다.

이와 같이 몫과 나머지를 구하는 방법을 조립제법이라고 한다.
예제 3.10 조립제법을 이용하여 다음 나눗셈의 몫과 나머지를 구하여라. \[ (x^{3} +3x^{2} -7)\div(x+1) \]
Sol.
조립제법을 이용하여 다음과 같이 계산한다.14
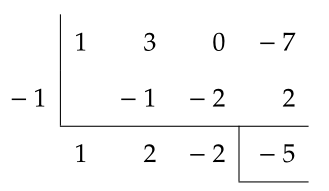 따라서 구하는 몫은 \(x^{2} +2x-2\)이고 나머지는 \(-5\)이다.
따라서 구하는 몫은 \(x^{2} +2x-2\)이고 나머지는 \(-5\)이다.
유제 3.11 조립제법을 이용하여 다음 나눗셈의 몫과 나머지를 구하여라.
- \((2x^{3} +x^{2} +3x-2)\div(x-1)\)
- \((x^{4} -2x^{2} +x+1)\div(x+2)\)
조립제법을 이용하여 다항식을 일차항의 계수가 \(1\)이 아닌 일차식으로 나눌 때의 몫과 나머지를 구하는 방법을 알아보자.
예제 3.12 조립제법을 이용하여 다음 나눗셈의 몫과 나머지를 구하여라. \[ (2x^{3} -5x^{2} -2x+3)\div(2x-1) \]
Sol.
조립제법을 이용하여 \(2x^{3} -5x^{2} -2x+3\)을 일차식 \(x-\frac{1}{2}\)로 나누었을 때 몫과 나머지를 구하면
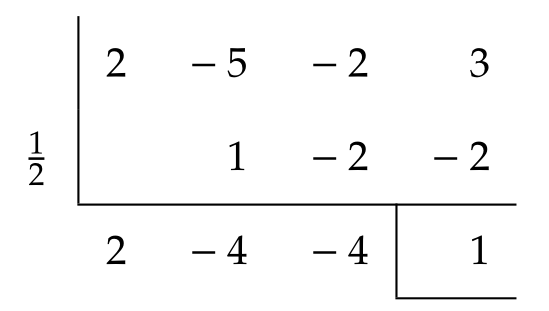 으로 몫은 \(2x^{2} -4x-4\)이고 나머지는 \(1\)이므로
\begin{align*}
2x^{3} -5x^{2} -2x+3& =\left(x-\frac{1}{2}\right)(2x^{2} -4x-4)+1 \\
& =(2x-1)\left(x^{2} -2x-2\right)+1
\end{align*}
이다. 따라서 몫은 \(x^{2} -2x-2\)이고 나머지는 \(1\)이다.
으로 몫은 \(2x^{2} -4x-4\)이고 나머지는 \(1\)이므로
\begin{align*}
2x^{3} -5x^{2} -2x+3& =\left(x-\frac{1}{2}\right)(2x^{2} -4x-4)+1 \\
& =(2x-1)\left(x^{2} -2x-2\right)+1
\end{align*}
이다. 따라서 몫은 \(x^{2} -2x-2\)이고 나머지는 \(1\)이다.
위의 결과로부터 어떤 다항식을 일차식 \(ax-b\)로 나누었을 때의 몫은 그 다항식을 일차식 \(x-\frac{b}{a}\)로 나누었을 때의 몫의 \(\frac{1}{a}\)이 됨을 알 수 있다.
유제 3.13 조립제법을 이용하여 다음 나눗셈의 몫과 나머지를 구하여라.
- \((2x^{3} -3x+2)\div(2x+1)\)
- \((4x^{4} +3x^{2} -2x+1)\div(2x-3)\)
항등식과 나머지정리
문자에 어떤 값을 대입하여도 항상 성립하는 등식을 그 문자에 대한 항등식이라고 한다. 예를 들어, \[ (a+b)^{3} =a^{3} +3a^{2} b+3ab^{2} +b^{3} \] 과 같은 곱셈 공식에서 등장한 등식은 모두 항등식이다.
등식 \(ax+b=0\)이 \(x\)에 대한 항등식이 될 조건을 알아보자. 등식 \(ax+b=0\)이 \(x\)에 대한 항등식이면 \(x\)에 어떤 값을 대입해도 등호가 성립한다. 따라서 \(x=0, x=1\)을 각각 대입하면 \(b=0, a+b=0\)이므로 \[ a=b=0 \] 이다. 역으로 \(a=b=0\)이면 등식 \(ax+b=0\)은 모든 \(x\)에 대하여 항상 성립한다. 그러므로 등식 \(ax+b=0\)이 \(x\)에 대한 항등식이 되기 위한 필요충분조건은 \(a=b=0\)이다.
이제, 등식 \(ax^{2}+bx+c=0\)이 \(x\)에 대한 항등식이 될 조건을 알아보자. 등식 \(ax^{2} +bx+c=0\)이 \(x\)에 대한 항등식이면 \(x=-1, x=0, x=1\)을 각각 대입하여 \[ a-b+c=0,\quad c=0, \quad a+b+c=0 \] 을 얻는다. 이 세 식을 연립하여 풀면 \[ a=b=c=0 \] 이다. 역으로 \(a=b=c=0\)이면 등식 \(ax^{2} +bx+c=0\)은 모든 \(x\)에 대하여 항상 성립한다. 따라서 등식 \(ax^{2}+bx+c=0\)이 \(x\)에 대한 항등식이 되기 위한 필요충분조건은 \(a=b=c=0\)이다.
Theorem 3.1.5 (항등식의 기본 성질)
등식 \(ax^{2} +bx+c=0\)이 \(x\)에 대한 항등식이 되기 위한 필요충분조건은
\[
a=b=c=0
\]
인 것이다.
유제 3.14 등식 \(ax^{2} +bx+c=a'x^{2} +b'x+c'\)이 \(x\)에 대한 항등식이 되기 위한 필요충분조건은 \(a=a', b=b', c=c'\)임을 보여라.
항등식에서 알지 못하는 계수의 값을 정하는 방법을 미정계수법이라고 한다. 대표적인 미정계수법에는 양변의 계수를 비교하여 계수의 값을 정하는 계수비교법과 적절한 수를 대입하여 계수의 값을 정하는 수치대입법이 있다.
예제 3.15 등식 \(x^{2} +4x+3=(x-1)^{2} +a(x-1)+b\)가 \(x\)에 대한 항등식이 되도록 \(a, b\)의 값을 정하여라.
Sol(계수비교법). 우변을 \(x\)에 대하여 내림차순으로 정리하면 \[ x^{2} +4x+3=x^{2} +(a-2)x+(-a+b+1) \] 이고 이 식의 양변의 계수를 서로 비교하여 \[ a-2=4, \quad -a+b+1=3 \] 를 얻는다. 이를 연립하여 \(a=6, b=8\)를 얻는다.
Sol(수치대입법). 주어진 식이 \(x\)에 대한 항등식이므로 \(x\)에 어떤 값을 대입하여도 등호가 성립해야만 한다. \(x=1\)을 대입하여 \(8=b\)를 얻고 이 결과와 \(x=0\)을 대입하여 \(3=1-a+8\), 즉 \(a=6\)을 얻는다.
유제 3.16 다음 등식이 \(x\)에 대한 항등식이 되도록 \(a, b, c\)의 값을 정하여라.
- \( (x+a)(x+2)=x^{2} +bx+2\)
- \( 2x^{2} +3x+7=a(x+1)^{2} +b(x+1)+c\)
예제 3.17 다항식 \(x^{3} +ax^{2} +bx+5\)를 \(x^{2} -x+2\)로 나누었을 때 나머지가 \(2x+3\)이 되도록 \(a, b\)의 값을 정하여라.
Sol(1).
다항식 \(x^{3}+ax^{2}+bx+5\)를 \(x^{2}-x+2\)로 나누어 보면
 으로 나머지가 \((a+b-1)x+(-2a+3)\)이고 따라서 \((a+b-1)x+(-2a+3)=2x+3\)를 얻는다.
이 등식은 \(x\)에 대한 항등식이므로
\[
a+b-1=2, \quad -2a+3=3
\]
이 성립하고 이로부터 \(a=0, b=3\)를 얻는다.
으로 나머지가 \((a+b-1)x+(-2a+3)\)이고 따라서 \((a+b-1)x+(-2a+3)=2x+3\)를 얻는다.
이 등식은 \(x\)에 대한 항등식이므로
\[
a+b-1=2, \quad -2a+3=3
\]
이 성립하고 이로부터 \(a=0, b=3\)를 얻는다.
Sol(2). 몫은 \(x\)의 계수가 \(1\)인 일차식일 수밖에 없으므로 몫을 \(x+c\)로 두어 다음과 같이 쓸 수 있다. \[ x^{3} +ax^{2} +bx+5=(x^{2} -x+2)(x+c)+(2x+3) \] 이 식의 양변에 \(x=0\)을 대입하여 \(5=2c+3\), 즉 \(c=1\)를 얻는다. 이 결과로부터 항등식 \[ x^{3} +ax^{2} +bx+5=x^{3} +3x+5 \] 를 얻으며 이로부터 \(a=0\)과 \(b=3\)을 얻는다.
유제 3.18 다항식 \(2x^{3} +ax^{2} +bx-1\)이 \(x^{2} +1\)로 나누어 떨어지도록 \(a, b\)의 값을 정하여라.
유제 3.19 두 이차식 \(P(x), Q(x)\)에 대하여, 만일 \[ P(x)Q(x)=0 \] 가 항등식이면 \(P(x)=0\)과 \(Q(x)=0\) 중 적어도 하나는 항등식임을 보여라.
상황에 따라 다항식의 나눗셈에 있어서 몫보다 나머지에 더 관심을 가질 때가 있다. 어떤 다항식을 일차식으로 나눌때, 나머지를 쉽게 구하는 방법인 나머지 정리를 알아보자.
예를 들어 다항식 \(x^{4} -2x^{2} +x-3\)을 일차식 \(x-2\)로 나누었을 때 나머지를 구하는 과정을 알아보자. 먼저 직접 나눗셈을 해보면
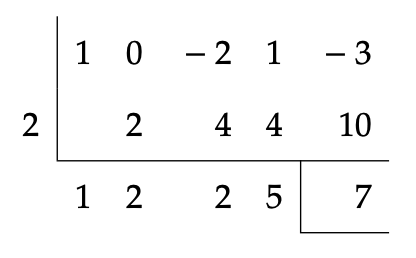 로부터 몫은 \(x^{3}+2x^{2}+2x+5\), 나머지는 \(7\)임을 알 수 있다. 이제 몫이 아니라 '나머지'에 관심이 더 있다고 생각하고 이 결과, 즉
\[
x^{4} -2x^{2} +x-3=(x-2)\left(x^{3}+2x^{2}+2x+5\right)+7
\]
를 살펴보자. 이 등식은 \(x\)에 대한 항등식이므로 \(x\)에 어떤 값을 대입하여도 성립하는 식이며, 특히 \(x=2\)를 대입하여도 성립하는 식이다.
로부터 몫은 \(x^{3}+2x^{2}+2x+5\), 나머지는 \(7\)임을 알 수 있다. 이제 몫이 아니라 '나머지'에 관심이 더 있다고 생각하고 이 결과, 즉
\[
x^{4} -2x^{2} +x-3=(x-2)\left(x^{3}+2x^{2}+2x+5\right)+7
\]
를 살펴보자. 이 등식은 \(x\)에 대한 항등식이므로 \(x\)에 어떤 값을 대입하여도 성립하는 식이며, 특히 \(x=2\)를 대입하여도 성립하는 식이다.
일반적으로 다항식 \(P(x)\)를 일차식 \(x-a\)로 나누었을 때 몫을 \(Q(x)\), 나머지를 상수 \(R\)로 두면15 \[ P(x)=(x-a)Q(x)+R \] 이 성립하며 이로부터 \[ P(a)=R \] 과 같다. 즉 다음과 같은 나머지정리가 성립한다.
Theorem 3.1.6 (나머지정리)
다항식 \(P(x)\)를 일차식 \(x-a\)로 나누었을 때의 나머지는 \(P(a)\)이다.
보기 다항식 \(P(x)=x^{4} -3x^{3} +x-4\)를 \(x-2\)로 나누었을 때 나머지는 \[ P(2)=2^{4} -3\cdot 2^{3} +2-4=-10 \] 이다.
유제 3.20 다항식 \(2x^{3} +x^{2} -3x+5\)를 다음 일차식으로 나누었을 때의 나머지를 구하여라.
- \( x-1\)
- \(x+2\)
유제 3.21 다항식을 일차식 \(ax+b\)로 나누었을 때의 나머지정리에 대해 설명하여라.
유제 3.22 다항식 \(2x^{3} -x^{2} +4x+1\)을 \(2x-1\)로 나누었을 때의 나머지를 구하여라.
다음 예제 및 유제들은 아주 기초적인 문제이다.
예제 3.23 다항식 \(P(x)=x^{3} +ax+2\)를 \(x-1\)로 나누었을 때의 나머지가 \(2\)가 되도록 \(a\)의 값을 정하여라
Sol. 나머지정리에 의해 다항식 \(P(x)\)를 \(x-1\)로 나누었을 때의 나머지는 \(P(1)\)과 같으므로 \[ P(1)=1+a+2=2 \] 이다. 따라서 \(a\)의 값은 \(-1\)이다.
유제 3.24 다항식 \(P(x)=x^{4}+ax^{2} -x+4\)를 \(x+2\)로 나누었을 때 나머지가 \(-2\)가 되도록 \(a\)의 값을 정하여라.
예제 3.25 다항식 \(P(x)\)를 \(x+1\)로 나누었을 때의 나머지는 \(1\)이고, \(x-2\)로 나누었을 때의 나머지는 \(4\)이다. 다항식 \(P(x)\)를 \((x+1)(x-2)\)로 나누었을 때 나머지를 구하여라.
Sol. 구하는 나머지를 \(ax+b\),몫을 \(Q(x)\)라고 하면16 \[ P(x)=(x+1)(x-2)Q(x)+ax+b \] 이다. 이 항등식의 양변에 \(x=-1, x=2\)를 각각 대입하여 나머지정리와 주어진 조건으로부터 두 개의 등식 \[ P(-1)=-a+b=1,\quad P(2)=2a+b=4 \] 를 얻는다. 이로부터 \(a=1, b=2\)를 얻고 따라서 따라서 구하는 나머지는 \(x+2\)이다.
유제 3.26 다항식 \(P(x)\)를 \(x+2\)로 나누었을 때 나머지는 \(-7\)이고, \(x-3\)으로 나누었을 때 나머지는 \(3\)이다. 다항식 \(P(x)\)를 \((x+2)(x-3)\)으로 나누었을 때 나머지를 구하여라.
나머지정리에 따르면 다항식 \(P(x)\)가 일차식 \(x-a\)로 나누어 떨어질 때, \(P(a)=0\)이다. 역으로 \(P(a)=0\)이면 \(P(x)\)는 일차식 \(x-a\)로 나누어 떨어진다. 즉 다음의 인수정리가 성립함을 알 수 있다.
Corollary 3.1.7 (인수정리)
다항식 \(P(x)\)가 일차식 \(x-a\)로 나누어 떨어지기 위한 필요충분조건은 \(P(a)=0\)인 것이다.
예제 3.27 다항식 \(2x^{3} +ax^{2} +2x+b\)가 \((x-1)(2x+1)\)로 나누어 떨어지도록 \(a, b\)의 값을 정하여라.
Sol. \(P(x)=2x^{3}+ax^{2}+2x+b\)로 두면 인수정리로부터 \[ P(1)=0,\quad P=\left(-\frac{1}{2}\right) =0 \] 를 얻는다. 즉 \[ 2+a+2+b=0,\quad -\frac{1}{4}+\frac{a}{4}-1+b=0 \] 이고 이로부터 \(a=-7, b=3\)임을 알 수 있다.
유제 3.28 다항식 \(ax^{3} +bx^{2} -7x+6\)이 \(x^{2} -3x+2\)로 나누어 떨어지도록 \(a, b\)의 값을 정하여라.
다항식 \(P(x)\)가 \(x-a\)로 나누어 떨어진다는 것은 \[ P(x)=(x-a)Q(x) \] 꼴로 나타낼 수 있다는 말이다. 이것은 \(P(x)\)가 \(x-a\)를 인수로 가진다는 뜻으로 다항식을 인수분해할 때 인수정리가 매우 유용하게 활용될 수 있음을 보여준다.
인수분해
이미 중학교에서 인수분해를 통해 이차방정식의 근을 찾을 수 있음을 살펴본 바 있다. 자연수를 소인수분해하면 그 수에 대한 성질을 보다 명확하게 파악할 수 있듯이 다항식을 인수분해하면 그 다항식을 잘 이해할 수 있다.
다항식을 인수분해하는 문제는 결코 쉬운 문제가 아니다. 여기서는 인수정리를 이용하여 인수분해하는 방법, 그리고 몇 가지 기초적인 인수분해 공식을 활용하여 인수분해하는 방법을 알아본다.
먼저 다항식을 인수분해하기 위해 그 다항식이 일차식을 인수로 가지는지를 인수정리를 이용하여 살펴볼 수 있다. 예를 들어 다항식 \(P(x)=x^{3} -3x+2\)를 인수분해하는 것을 생각해보자. 다항식 \(P(x)\)는 최고차항의 계수가 \(1\)이므로 만일 이 다항식이 일차식을 인수로 가진다면
\[
x^{3} -3x+2=(x-a)(x^{2} +bx+c)
\]
와 같이 일차식과 이차식의 곱으로 인수분해된다. 이 등식은 \(x\)에 대한 항등식이므로 양변의 상수항을 비교하면
\[
-ac=2
\]
이다. 따라서 \(a\)가 정수라면 그 값은17
\[
1,\quad -1,\quad 2,\quad -2
\]
가운데 하나가 된다. 이 값 가운데 \(1\)을 \(P(x)\)에 대입하여 보면
\[
P(1)=0
\]
이므로 인수정리에 의하여 \(P(x)\)는 \(x-1\)을 인수로 가진다. 이제 조립제법을 이용하면
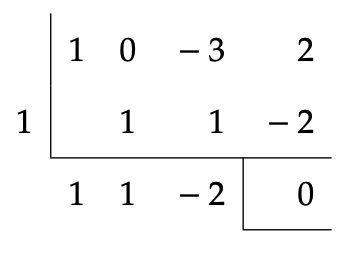 로 그 몫은 \(x^{2} +x-2\)이므로 \(x^{3} -3x+2\)는 다음과 같이 인수분해된다.
로 그 몫은 \(x^{2} +x-2\)이므로 \(x^{3} -3x+2\)는 다음과 같이 인수분해된다.
이처럼 삼차 이상의 다항식에서 인수정리를 이용하여 일차식의 인수를 찾으면 조립제법을 활용하여 인수분해를 할 수 있다.18
유제 3.29 다음 다항식을 인수분해하여라.
- \(x^{3} -1\)
- \(x^{3} -x^{2} -5x-3\)
- \(x^{4} -2x^{3} +x-2\)
- \(x^{4} -3x^{3} +3x^{2} -3x+2\)
이번에는 최고차항의 계수가 \(1\)이 아닌 다항식을 인수분해할 때 인수정리와 조립제법을 어떻게 이용하는지 알아보자.
예를 들어 다항식 \(P(x)=2x^{3} +x^{2} +x-1\)의 인수분해를 시도해보자. 만일 다항식 \(P(x)\)가 인수분해된다면
\[
2x^{3} +x^{2} +x-1=(ax-b)(cx^{2} +dx+e)
\]
꼴이다. 이 등식은 \(x\)에 대한 항등식이므로 \(x^{3}\)의 계수와 상수항을 비교했을 때
\[
ac=2,\quad be=1
\]
이 성립해야만 함을 알 수 있다. 따라서 만일 \(a\)와 \(b\)가 정수라면, \(a\)는 \(2\)의 약수이고 \(b\)는 \(1\)의 약수임을 알 수 있으며 결국 \(\frac{b}{a}\)의 값은 19
\[
1,\quad -1,\quad \frac{1}{2} ,\quad -\frac{1}{2}
\]
중 하나라는 것을 알 수 있다. 즉 이 값들이 바로 인수정리를 통해 \(P(x)\)의 일차인수를 찾을 때 사용하는 방정식 \(P(x)=0\)의 근의 후보인 것이다. 이 값들을 \(P(x)\)에 차례로 대입하여 보면 \(P\left(\frac{1}{2}\right)=0\)임을 확인할 수 있고 인수정리로부터 \(P(x)\)는 \(x-\frac{1}{2}\)을 인수로 가짐을 알 수 있다. 이제 조립제법을 이용하면
 로 \(P(x)\)를 \(x-\frac{1}{2}\)로 나누었을 때의 몫은 \(2x^{2}+2x+2\)임을 얻는다. 따라서 구하는 식은
\[
2x^{3} +x^{2} +x-1=\left(x-\frac{1}{2}\right)\left(2x^{2} +2x+2\right)=(2x-1)\left(x^{2} +x+1\right)
\]
이다.
로 \(P(x)\)를 \(x-\frac{1}{2}\)로 나누었을 때의 몫은 \(2x^{2}+2x+2\)임을 얻는다. 따라서 구하는 식은
\[
2x^{3} +x^{2} +x-1=\left(x-\frac{1}{2}\right)\left(2x^{2} +2x+2\right)=(2x-1)\left(x^{2} +x+1\right)
\]
이다.
위의 인수분해 과정에서 가장 중요한 장면은 인수정리를 사용하는 장면이다. 이는 곧 주어진 다항식의 한 근을 찾아내는 장면이라 할 수 있는데 무수히 많은 후보들을 대책없이 대입하는 것이 아니라20 \[ \pm\frac{(\text{상수항의 약수})}{(\text{최고차항 계수의 약수})} \] 를 우선적으로 대입하여 그 근을 찾아내는 것이 그 과정의 핵심적인 부분이라 할 수 있겠다.
유제 3.30 다음 다항식을 인수분해하여라.
- \(2x^{3} -x^{2} +x+1\)
- \(3x^{3} +2x^{2} -4x+1\)
이제 몇 가지 기초적인 공식들을 활용한 인수분해를 알아보자. 인수분해되는 이차식이나 삼차식은 반드시 일차식을 인수로 가진다. 21 그러나 사차식은 인수분해된다고 해서 반드시 일차식을 인수로 가지는 것은 아니다. 예를 들어 두 항등식 \begin{align*} &x^{4} +4x^{2} +3=(x^{2} +1)(x^{2} +3), \\ &x^{4} +x^{2} +1=(x^{2} +x+1)(x^{2} -x+1) \end{align*} 의 경우를 살펴보자. 이 식의 좌변에 있는 사차식을 인수분해한 것이 우변인데, 우변의 이차식들은 더 이상 인수분해되지 않는다. 이는 좌변의 사차식들은 인수정리를 이용하여 인수분해할 수 없다는 것을 알 수 있다.
이와 같이 인수정리를 이용하여 인수분해할 수 없는 사차식 가운데 먼저 사차항, 이차항, 상수항으로 이루어진 \(ax^{4} +bx^{2} +c\)꼴의 다항식을 인수분해하여 보자.
예제 3.31 다항식 \(x^{4} +4x^{2} +3\)을 인수분해하여라.
Sol. \(x^{2} =X\)로 놓으면 주어진 다항식은 \begin{align*} x^{4} +4x^{2} +3&=X^{2} +4X+3\\ & =(X+1)(X+3) \end{align*} 로 쓸 수 있다.22 여기서 \(X\)에 \(x^{2}\)을 대입하여 \[ x^{4} +4x^{2} +3=(x^{2} +1)(x^{2} +3) \] 를 얻는다.
유제 3.32 다음 다항식을 인수분해하여라.
- \(x^{4} +5x^{2} +4\)
- \(2x^{4} +7x^{2} +6\)
- \(5x^{4} +16x^{2} +3\)
- \(2x^{4} +3x^{2} +1\)
예제 3.33 다항식 \(x^{4} +x^{2} +1\)을 인수분해하여라.
Sol. \(x^{2} =X\)로 치환하는 것을 생각해보니, 치환하여 얻은 이차식이 인수분해되지 않는다는 것을 바로 알 수 있다. 이 경우에는 이차항을 적절하게 더하고 빼서 \(A^{2}-B^{2}\) 꼴로 변형한다. 이 예제의 경우에는 \(x^{2}\)을 더하고 빼서 \(A^{2}-B^{2}\) 꼴로 식을 변형하여 다음과 같이 인수분해한다. \begin{align*} x^{4} +x^{2} +1&= x^{4} +2x^{2} +1-x^{2} \\ & =(x^{4} +2x^{2} +1)-x^{2} \\ & =(x^{2} +1)^{2} -x^{2} \\ & =(x^{2} +x+1)(x^{2} -x+1) \end{align*}
유제 3.34 다음 다항식을 인수분해하여라.
- \(x^{4} +3x^{2} +4\)
- \(x^{4} -6x^{2} +1\)
- \(x^{4} +2x^{2} +9\)
- \(x^{4} -9x^{2} +16\)
두 개 이상의 문자를 포함하는 다항식은 한 문자에 대하여 내림차순으로 정리하여 인수분해하는 것이 요령이다.
예제 3.35 다음 다항식을 인수분해하여라.
- \(ab+bc-cd-da\)
- \(2x^{2} +5xy+3y^{2} +3x+5y-2\)
Sol.
- \(a\)에 대하여 내림차순으로 정리하여 다음과 같이 인수분해한다. \begin{align*} ab+bc-cd-da&=a(b-d)+bc-cd \\ & =a(b-d)+c(b-d)\\ & =(a+c)(b-d) \end{align*}
- \(x\)에 대하여 내림차순으로 정리하여 다음과 같이 인수분해한다. \begin{align*} & 2x^{2} +5xy+3y^{2} +3x+5y-2\\ &\phantom{MMM} =2x^{2} +(5y+3)x+(3y^{2} +5y-2) \\ &\phantom{MMM} =2x^{2} +(5y+3)x+(y+2)(3y-1) \\ &\phantom{MMM} =(x+y+2)(2x+3y-1) \end{align*}
유제 3.36 다음 다항식을 인수분해하여라.
- \(ac+2bc-2bd-ad\)
- \(3x^{2} -2xy-y^{2} -5x+y+2\)
- \(a^{2} +b^{2} +ac-bc-2ab\)
- \(x^{2} +3xy+2y^{2} -x-3y-2\)
인수분해는 물론 다항식의 전개 과정을 역으로 생각할 수 있다. 다음은 곱셈 공식에서 좌변과 우변을 바꾸어 써서 얻은 공식이다.
Theorem 3.1.8 (인수분해 공식)
- \(a^{2} +b^{2} +c^{2} +2ab+2bc+2ca=(a+b+c)^{2}\)
- \( a^{3} +3a^{2} b+3ab^{2} +b^{3} =(a+b)^{3} ,\)
\( a^{3} -3a^{2} b+3ab^{2} -b^{3} =(a-b)^{3} \) - \( a^{3} +b^{3} =(a+b)(a^{2} -ab+b^{2} ) ,\)
\( a^{3} -b^{3} =(a-b)(a^{2} +ab+b^{2} ) \)
유제 3.37 인수분해 공식을 이용하여 다음 다항식을 인수분해하여라.
- \(x^{3} -8\)
- \(x^{3} +6x^{2} +12x+8\)
- \( 27x^{3} +1\)
- \(x^{3} -6x^{2} +12x-8\)
- \(8x^{3} -y^{3} \)
- \( a^{2} +b^{2} +c^{2} -2ab+2bc-2ca\)
물론 다항식은 여러 가지 방법으로 인수분해할 수 있다. 실제로 위 인수분해 공식들을 이용하여 인수분해 할 수 있는 다항식은 모두 인수정리를 이용하여 인수분해할 수 있다.
유제 3.38 다음 다항식을 인수분해하여라.
- \(x^{4} -1\)
- \(x^{3} -8y^{3}\)
- \(x^{4} -4\)
- \(x^{3} -3x^{2} y+3xy^{2} -y^{3}\)
- 다항식은 여러모로 정수와 유사한 구조를 갖고 있다.
- 하나의 항으로만 이루어진 다항식은 단항식(monomial)이라 부르기도 한다.
- \(x\)에 대한 다항식, \(x, y\)에 대한 다항식 등과 같이 말하는 것도 좋다.
- 상수 다항식이 아닌 다항식이 있을 때, 그 다항식의 항들이 갖는 차수 중에서 가장 큰 것을 그 다항식의 차수라 한다. \(-xy^{2}+x^{2}+a^{4}y^{2}+x\)의 차수는 무엇일까?
- 왠지 내림차순으로 정리하는 것이 마음이 편한 것 같긴한데...
- 내림차순으로 예쁘게 정리하는 센스는 기본
- 무척 당연한 이야기지만 문자를 계산함에 있어, 그 문자가 무엇을 나타내는가에 계산에 관한 어떤 성질들을 사용할 수 있는지가 달려있다.
- 사실 중요한 건, 각 항의 계수들이니 세로셈에 문자를 다 써놓을 필요는 없어보인다. 잉크를 낭비한 건 아닐까...
- 덧셈의 역원이 있으니 뺄셈을 잘 정의할 수 있다.
- 이정도의 공식은 쌩기초!
- 분배법칙의 경우 '곱셈에 대한 성질'이라기보단 '덧셈과 곱셈을 연결짓는 성질'이라 해야겠지만...
- 정확하게는 \(2x^{2} +5x-5\)를 \(x+3\)으로 나누었을 때의 몫과 나머지.
- 역시 계수만을 이용하는 것이 절약정신에 부합하는 것이다!
- 나누어지는 다항식의 계수를 나열할 때, 다항식의 차수별로 모든 계수를 빠짐없이 써야함에 유의하자. 즉, 계수가 \(0\)일 때에도 \(0\)을 쓰는 것을 빠뜨리지 말자.
- 다항식을 일차식으로 나누었을 때의 나머지는 상수.
- 이차식으로 나누었으니 나머지는 일차식 또는 상수이다.
- 운이 좋다면 정수일 것이다.
- 물론 차수가 3, 4, \(n\)인 다항식을 각각 삼차, 사차, \(n\)차 다항식이라고 한다.
- 운이 좋다면 정수일 것이다(항상 운이 좋은 느낌?).
- '다항식 \(P(x)\)의 근'이란 방정식 \(P(x)=0\)의 근이다.
- 어떤 다항식이 인수분해가 되는지, 되지 않는지는 인수분해를 '어느 동네'에서 하는가에 달려있다. 예를 들어 이차식 \(x^{2}+1\)은 '실수계수 다항식 동네'에서는 더 낮은 차수의 다항식들로 인수분해할 수 없다. 그러나 이 다항식은 물론 '복소계수 다항식 동네'에서 \[x^{2}+1=(x+i)(x-i)\]로 인수분해된다. 따라서 인수분해를 '어느 동네'에서 하느냐는 사실 아주 중요한 문제라 할 수 있다.
앞으로 별다른 언급이 없이 어떤 다항식을 인수분해하라고 하면 우선적으로 유리수 계수 다항식 범위에서 하는 것을 생각한다. 그러나 유리계수 범위에서 인수분해를 한 후에도 주어진 다항식이 실계수 범위에서는 어떻게 인수분해되는지, 복소계수 범위에서는 어떻게 인수분해되는지 슬쩍 생각해보는 것도 나쁘지 않다. - \(x^{2} =X\)로 치환했을 때, \(X\)에 대한 이차식이 인수분해되는 경우이다.