이 글은 현재는 절판된 Serge Lang의 선형대수 교재 제2판([1], VII, §6)의 내용을 토대로 쓴 것이다. 퍼가지 마시라.
이 글에서는 행렬식을 한 도형의 체적으로 이해하는 이야기를 소개한다. 먼저 2-차원의 경우를 논할텐데, '체적(volume)'이라는 용어를 2-차원 도형의 넓이를 일컬을 때에도 그냥 사용하고자 한다. 또한 '\(\operatorname{Vol}\)'와 같은 기호를 이용하여 넓이를 나타내기도 할 것이다. 물론 이 기호를 일반적인 고차원 도형의 체적을 나타내는 기호로도 쓸 것이다.
먼저 두 벡터 \(v, w\)로 생성한 평행사변형을 생각해보자. 물론 이 평행사변형은 \[ t_{1}v+t_{2}w\quad (0\leq t_{i}\leq 1) \] 꼴의 일차결합으로 표현되는 모든 벡터를 모아놓은 집합을 일컫는다.
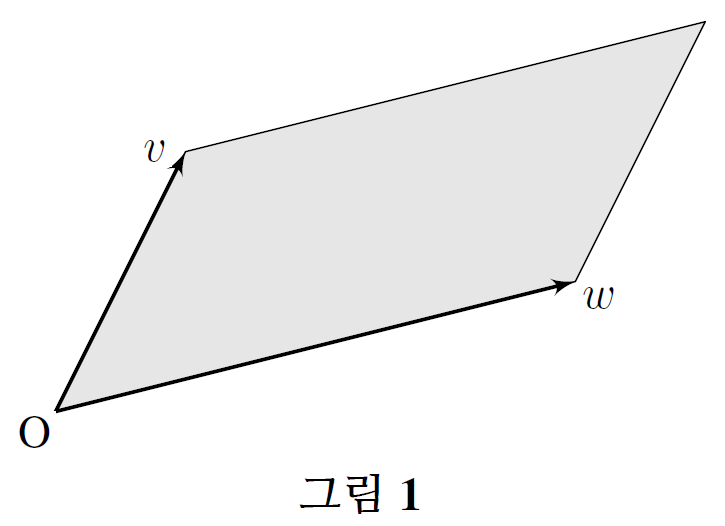
두 벡터 \(v, w\)를 열벡터로 생각하여 행렬식 \(\det(v, w)\)를 생각할 수 있다. 이 행렬식은 두 벡터가 나란하지만 않다면, 양수 혹은 음수의 값을 가질 것이며 다음 등식을 만족시킨다. \[ \det(v, w)=-\det(w, v) \] 따라서 행렬식 그 자체를 지금 생각하는 평행사변형의 넓이라고 바로 말할 수는 없다. 왜냐하면 우리는 넓이 혹은 부피로 생각하는 값을 항상 음이 아닌 실수값으로 생각하기 때문이다. 그러나 다음을 보일 수 있다.
Theorem.1.
두 벡터 \(v, w\)로 생성한 평행사변형의 넓이는 그 두 벡터로 만든 행렬식의 절댓값인 \(\vert\det(v, w)\,\vert\)와 같다.
정리 1을 보이기 위해 방향이 있는 넓이(oriented area)라는 개념을 소개한다. 두 벡터 \(v\)와 \(w\)로 생성한 평행사변형을 \(P(v, w)\)로 나타내자. 그리고 실숫값 \(\operatorname{Vol}_{\mathrm{O}}(v, w)\)를 정의하되, \(\det(v,w)\geq 0\)일때는 그 값을 \(P(v, w)\)의 넓이로, \(\det(v, w)<0\)일때는 그 값을 \(P(v, w)\)의 넓이에 \(-1\)을 곱한 값으로 정의하자. 그러면 \(\operatorname{Vol}_{\mathrm{O}}(v, w)\)가 행렬식 \(\det(v, w)\)와 동일한 부호를 가짐을 바로 알 수 있다. 실수 \(\operatorname{Vol}_{\mathrm{O}}(v, w)\)를 방향이 있는 넓이라고 부르자. 또한 \(v, w\)로 생성된 평행사변형의 넓이는 \(\operatorname{Vol}(v, w)\)로 나타내자. 따라서 \(\operatorname{Vol}_{\mathrm{O}}(v, w)=\operatorname{Vol}(v, w)\) 혹은 \(\operatorname{Vol}_{\mathrm{O}}(v, w)=-\operatorname{Vol}(v, w)\)이다.
정리 1을 증명하기 위해서는 다음을 보이면 충분하다.
Proposition.
방향이 있는 넓이는 행렬식의 값과 일치한다. 즉
\[
\operatorname{Vol}_{\mathrm{O}}(v, w)=\det(v, w)
\]
가 성립한다.
이제 위의 명제를 증명하기 위해 \(\operatorname{Vol}_{\mathrm{O}}\)이 행렬식을 규정하는 세 가지 성질을 만족시킨다는 것을 보이자. 즉
- 변수 \(v\)와 \(w\) 각각에 대하여 \(\operatorname{Vol}_{\mathrm{O}}\)은 선형이다.
- 임의의 \(v\)에 대하여 \(\operatorname{Vol}_{\mathrm{O}}(v, v)=0\)이다.
- \(e_{1}, e_{2}\)가 표준기저일 때, \(\operatorname{Vol}_{\mathrm{O}}(e_{1}, e_{2})=1\)이다.
임을 보이자. 선형대수를 공부했다면, 위의 세 가지 조건을 만족시키는 \(\mathbb{R}^{2}\times\mathbb{R}^{2}\)에서 \(\mathbb{R}\)로의 함수가 유일하게 존재하며, 그 함수를 \(\det\)로 정의함을 알고 있을 것이다. 이 글을 읽는 독자를 위해 간략히 이 내용을 간략히 소개해본다. 위의 세 가지 조건을 만족시키는 함수 \(G\)가 있다고 하자. 그러면 임의의 두 벡터 \[ v=ae_{1}+ce_{2},\quad w=be_{1}+de_{2} \] 에 대하여, \[ G(ae_{1}+ce_{2}, be_{1}+de_{2}) = abG(e_{1}, e_{1})+ adG(e_{1}, e_{2})+cbG(e_{2}, e_{1}) + cdG(e_{2}, e_{2}) \] 가 성립한다. 여기서 우변의 첫 항과 마지막 항은 \(0\)임을 바로 알 수 있다. 또한 간단한 관찰을 통해 \[ G(e_{2}, e_{1})=-G(e_{1}, e_{2}) \] 임을 확인할 수 있고 따라서 \[ G(v, w)=(ad-bc)G(e_{1}, e_{2})=ad-bc \] 를 얻는다. 즉 \(\mathbb{R}^{2}\times\mathbb{R}^{2}\)에서 \(\mathbb{R}\)로의 함수 \(G\)는 \(\det\)와 같다.
이제 \(\operatorname{Vol}_{\mathrm{O}}\)이 위의 세 가지 조건을 만족시킨다는 것을 보이기 위해 넓이(혹은 부피)가 갖는 다음의 간단한 성질 몇 가지를 활용하려 한다.
- 선분의 넓이는 \(0\)과 같다.
- 만일 \(A\)가 어떤 영역일 때, \(A\)를 평행이동하여 얻은 영역 \(A_{w}=\{ v+w\mid v\in A\}\)의 넓이는 \(A\)의 넓이와 같다.
- 두 영역 \(A, B\)가 서로 만나지 않거나 혹은 만나더라도 \(A\cap B\)의 넓이가 \(0\)이면 \[ \operatorname{Vol}(A\cup B)=\operatorname{Vol}(A)+\operatorname{Vol}(B) \] 이다.
이제 \(\operatorname{Vol}_{\mathrm{O}}\)을 생각해보자. 행렬식을 규정하는 세 가지 성질 중 두 번째, 세 번째 성질을 \(\operatorname{Vol}_{\mathrm{O}}\)이 만족시킨다는 것은 자명하다. 즉 \(v, v\)로 생성된 평행사변형은 하나의 선분이므로 이의 \(2\)-차원 넓이는 \(0\)과 같고 따라서 \(\operatorname{Vol}_{\mathrm{O}}(v, v)=0\)이다. 세 번째 성질을 확인해보자. 표준기저 \(e_{1}, e_{2}\)로 생성한 평행사변형은 단위정사각형으로 넓이 \(1\)을 갖는다. 따라서 \[ \operatorname{Vol}_{\mathrm{O}}(e_{1}, e_{2})=1 \] 임을 얻는다. \(\operatorname{Vol}_{\mathrm{O}}\)이 행렬식을 규정하는 첫 번째 성질을 만족시킨다는 것은 다른 두 성질을 확인하는 것에 비하여 품이 더 많이 든다. 유클리드 공간의 벡터를 다루는데 조금은 익숙한 것이 다음 내용을 읽는데 도움이 될 것이다.
먼저 다음의 보조정리를 보이자.
Lemma.2.
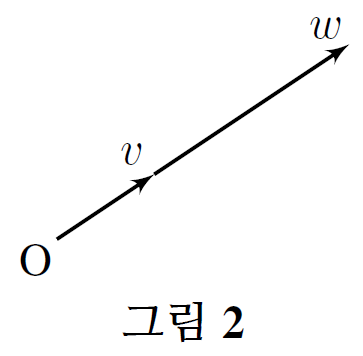
만일 \(v, w\)가 일차종속이면 \(\operatorname{Vol}_{\mathrm{O}}(v, w)=0\)이다.
Proof. 가정에 의해 \(a\neq 0\) 혹은 \(b\neq 0\)인 두 스칼라 \(a, b\)를 이용하여 \[ av+bw=0 \] 로 쓸 수 있다. 일반성을 잃지 않고 \(a\neq 0\)이라 하면 \[ v=-\frac{b}{a}w=c w \] 꼴로 쓸 수 있으며 이는 \(v\)와 \(w\)가 동일한 직선 상에 있다는 뜻이 된다. 따라서 \(v, w\)로 생성된 평행사변형은 하나의 선분이 된다(그림 2). 따라서 \(\operatorname{Vol}_{\mathrm{O}}(v, w)=0\)이다.
한편 \(v, w\)가 일차종속일 때는 \(\det(v, w)=0\)임을 알고 있으므로 일차종속인 두 벡터에 관해서는 우리가 증명하고자하는 명제는 증명이 된 것과 같다. 이제 다음으로 살펴볼 보조정리들에서는 \(v, w\)가 일차독립임을 가정한다.
Lemma.3.
일차독립인 \(v, w\)와 자연수 \(n\)에 대하여
\[
\operatorname{Vol}(nv, w)=n\cdot\operatorname{Vol}(v, w)
\]
이 성립한다.
Proof. 두 벡터 \(nv, w\)로 생성된 평행사변형은 그림 3과 같이 \(n\)개의 평행사변형으로 이루어져있다.
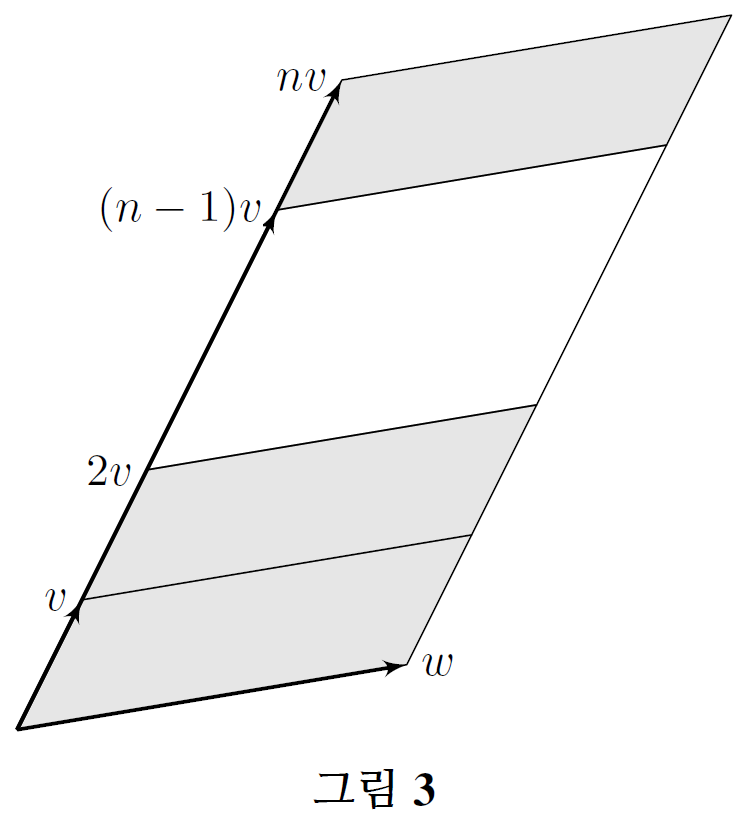
이 \(n\)개의 평행사변형은 각각 \(P(v, w)\)를 \(v, 2v, \ldots, (n-1)v\)를 이용하여 평행이동함으로써 얻은 것이므로 이들 각각의 넓이는 모두 \(P(v, w)\)의 넓이와 같다. 또한 이 평행사변형들이 다른 평행사변형들과는 기껏해야 선분들만 공유하므로 원하는 결론인 \[ \operatorname{Vol}(nv, w)=n\cdot\operatorname{Vol}(v, w) \] 를 얻는다.
Corollary.4.
일차독립인 \(v, w\)와 자연수 \(n\)에 대하여
\[
\operatorname{Vol}\left(\frac{1}{n}v, w\right)=\frac{1}{n}\operatorname{Vol}(v, w)
\]
가 성립한다. 또한 \(m, n\)이 모두 자연수이면
\[
\operatorname{Vol}\left(\frac{m}{n}v, w\right)=\frac{m}{n}\operatorname{Vol}(v, w)
\]
이 성립한다.
Proof. \(v_{1}=(1/n)v\)로 두면 바로 위의 보조정리로부터 \[ \operatorname{Vol}(nv_{1}, w)=n\operatorname{Vol}(v_{1}, w) \] 를 얻는다. 이는, 등식 \(nv_{1}=v\)를 생각할 때, 지금 증명하고 있는 첫 번째 등식을 다시 쓴 것과 동일한 식임을 알 수 있다. 두 번째 등식을 보이기 위해 \(m/n=m\cdot 1/n\)으로 두고 방금 보인 첫 번째 등식을 활용하면 \begin{align*} \operatorname{Vol}\left(m\cdot\frac{1}{n}v, w\right)&=m\operatorname{Vol}\left(\frac{1}{n}v, w\right)\\ &=m\cdot\frac{1}{n}\operatorname{Vol}\left(v, w\right) \\ &=\frac{m}{n}\operatorname{Vol}\left(v, w\right) \end{align*} 를 얻는다.
Lemma.5.
\(\operatorname{Vol}(-v, w)=\operatorname{Vol}(v, w).\)
Proof. 두 벡터 \(-v, w\)로 생성된 평행사변형은 평행사변형 \(P(v, w)\)를 \(-v\)로 평행이동한 것과 같다. 따라서 \(P(v, w)\)와 \(P(-v, w)\)는 동일한 넓이를 갖는다(그림 4).
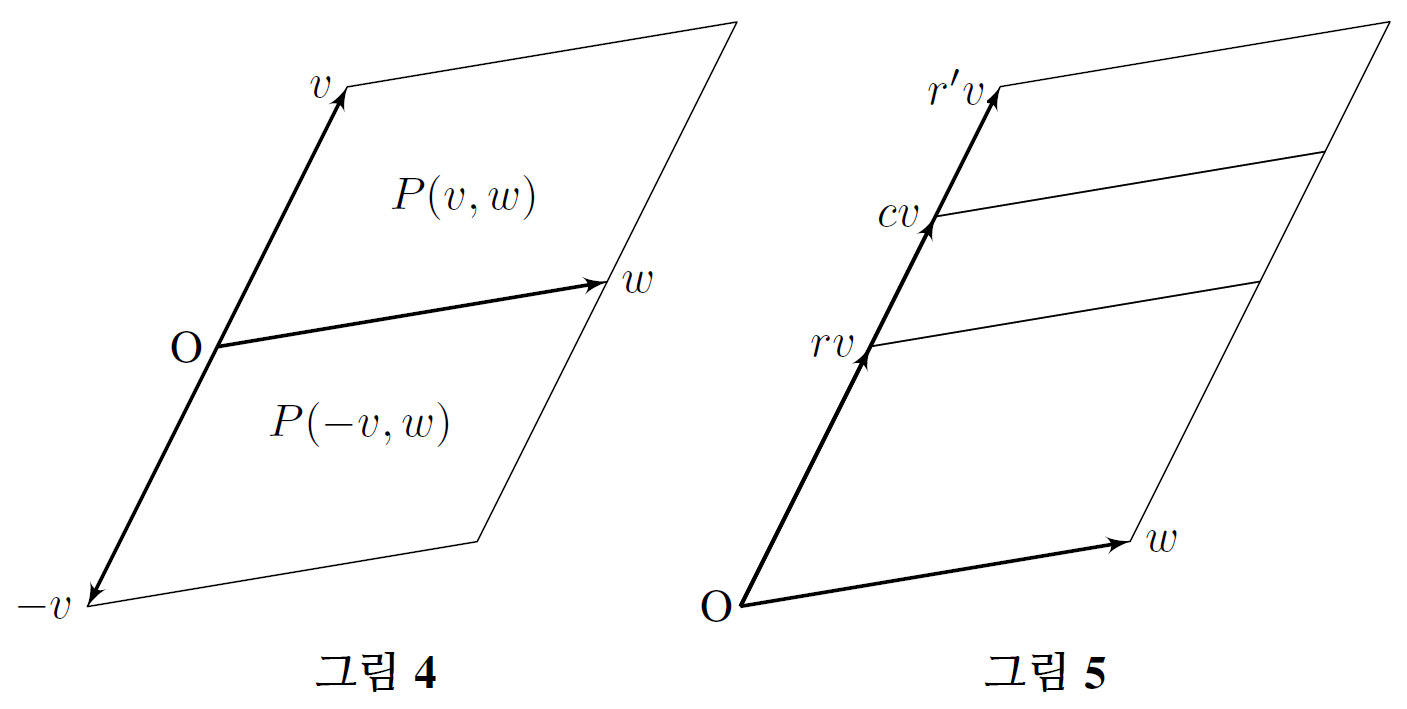
Lemma.6.
임의의 양의 실수 \(c\)에 대하여
\[
\operatorname{Vol}(cv, w)=c\cdot\operatorname{Vol}(v, w)
\]
가 성립한다.
Proof. 두 유리수 \(r, r'\)이 \(0< r < c < r'\)을 만족시킨다고 하자(그림 5). 그러면 \[ P(rv, w)\subset P(cv, w)\subset P(r'v, w) \] 가 성립한다. 따라서 따름정리 4로부터 \begin{align*} r\cdot\operatorname{Vol}(v, w)&=\operatorname{Vol}(rv, w) \\ &\leq \operatorname{Vol}(cv, w) \\ &\leq \operatorname{Vol}(r'v, w) \\ &=r'\cdot\operatorname{Vol}(v, w) \end{align*} 를 얻는다. \(r\)과 \(r'\)는 각각은 \(c\)와 얼마든지 가까워질 수 있으므로 \(r\)과 \(r'\)이 \(c\)로 가도록 극한을 취하여 \[ \operatorname{Vol}(cv, w)=c\cdot\operatorname{Vol}(v, w) \] 를 얻는다.
보조정리 5와 보조정리 6으로부터 임의의 실수 \(c\)와 임의의 두 벡터 \(v, w\)에 대하여 \[ \operatorname{Vol}_{\mathrm{O}}(cv, w)=c\cdot\operatorname{Vol}_{\mathrm{O}}(v, w) \] 가 성립함을 보일 수 있다. 만일 \(v, w\)가 일차종속이면 위 식의 양변은 \(0\)이다. 만일 \(v, w\)가 일차독립이라면 \(\operatorname{Vol}_{\mathrm{O}}\)의 정의와 보조정리 5와 보조정리 6을 이용한다. \(\det(v, w)=c\)이고 \(c\)가 음수일 때, \(c=-d\)로 두자. 그러면 \(\det(cv, w)\leq 0\)이며 따라서 \begin{align*} \operatorname{Vol}_{\mathrm{O}}(cv, w)=-\operatorname{Vol}(cv, w)&=-\operatorname{Vol}(-dv, w) \\ &= -\operatorname{Vol}(dv, w) \\ &=-d\operatorname{Vol}(v, w) \\ &=\operatorname{Vol}(v, w)=c\operatorname{Vol}_{\mathrm{O}}(v, w) \end{align*} 를 얻는다. 유사한 방법을 통해 \(\det(v, w)\leq 0\)인 경우를 증명할 수 있다. 따라서 \(\operatorname{Vol}_{\mathrm{O}}\)의 선형성의 조건 중 하나를 보였다. 물론 \(\operatorname{Vol}_{\mathrm{O}}(v, w)\)의 변수 \(w\)에 관해서도 마찬가지이다. 즉 \[ \operatorname{Vol}_{\mathrm{O}}(v, cw)=c\cdot\operatorname{Vol}_{\mathrm{O}}(v, w) \] 가 성립한다.
이제 선형성에 관한 나머지 조건을 보이기 위해 다음의 보조정리를 보이자.
Lemma.7.
두 벡터 \(v, w\)가 일차독립이라 하자. 그러면
\[
\operatorname{Vol}(v+w, w)=\operatorname{Vol}(v, w)
\]
이 성립한다.
Proof. 두 벡터 \(v\)와 \(w\)로 생성된 평행사변형의 넓이가 \(v+w\)와 \(w\)로 생성된 평행서변형의 넓이와 일치함을 보여야한다.

그림 6에서 알 수 있듯이 \(v, w\)로 생성된 평행사변형은 두 삼각형 \(A, B\)로 이루어져 있다. 그리고 \(v+w, w\)로 생성된 평행사변형은 삼각형 \(A\)를 \(w\)로 평행이동하여 얻은 삼각형 \(A+w\)와 삼각형 \(B\)로 이루어져 있다. 두 삼각형 \(A\)와 \(A+w\)가 동일한 넓이를 가지므로 \[ \operatorname{Vol}(v, w)=\operatorname{Vol}(A)+\operatorname{Vol}(B)=\operatorname{Vol}(A+w)+\operatorname{Vol}(B)=\operatorname{Vol}(v+w, w) \] 를 얻는다.
이제 선형성에 관한 두 번째 조건을 보이자. 평면에 놓인 벡터 \(w\)가 \(0\)이 아닌 벡터라 하자. 그리고 \(\{v, w\}\)가 동일한 평면의 기저가 되도록 \(v\)를 택하고, 임의의 스칼라 \(c, d\)에 대하여 \begin{equation}\label{eq:01} \operatorname{Vol}_{\mathrm{O}}(cv+dw, w)=c\cdot\operatorname{Vol}_{\mathrm{O}}(v, w) \tag{1} \end{equation} 가 성립함을 보이자. 만일 \(d=0\)이면 딱히 증명할 것이 없다. 만일 \(d\neq0\)이면 앞서 살펴본 관찰을 활용하여 \[ d\cdot\operatorname{Vol}_{\mathrm{O}}(cv+dw, w)=\operatorname{Vol}_{\mathrm{O}}(cv+dw, dw)=c\cdot\operatorname{Vol}_{\mathrm{O}}(v, dw)=cd\cdot\operatorname{Vol}_{\mathrm{O}}(v, w) \] 를 얻으며 \(d\)를 소거하여 관계식 (1)을 얻는다. 관계식 (1)로부터 지금 보이고자 하는 \(\operatorname{Vol}_{\mathrm{O}}\)의 선형성에 관한 조건을 만족시킨다는 것을 얻을 수 있다. 실제로 \[ v_{1}=c_{1}v+d_{1}w,\quad v_{2}=c_{2}v+d_{2}w \] 로 두면, \begin{align*} \operatorname{Vol}_{\mathrm{O}}(v_{1}+v_{2}, w)&=\operatorname{Vol}_{\mathrm{O}}\left((c_{1}+c_{2})v+(d_{1}+d_{2})w, w\right) \\ &=(c_{1}+c_{2})\operatorname{Vol}_{\mathrm{O}}(v, w) \\ &=c_{1}\operatorname{Vol}_{\mathrm{O}}(v, w)+c_{2}\operatorname{Vol}_{\mathrm{O}}(v, w) \\ &=\operatorname{Vol}_{\mathrm{O}}(v_{1}, w)+\operatorname{Vol}_{\mathrm{O}}(v_{2}, w) \end{align*} 가 성립한다.
지금까지 함수 \(\operatorname{Vol}_{\mathrm{O}}\)이 행렬식을 규정하는 세 가지 조건을 모두 만족시킨다는 것을 확인하였다. 즉 \[ \operatorname{Vol}_{\mathrm{O}}(v, w)=\det(v, w) \] 가 성립한다.
Remark.1. 지금까지 살펴본 증명이 다소 길다는 느낌을 받았을 수 있다. 그러나 각 증명 단계의 내용은 꽤 단순하다 할 수 있다. 더욱이 각 단계의 논의를 고차원으로 일반화하려 할 때, 지금까지의 논증과 거의 동일한 방식으로 그 내용을 증명할 수 있다. 이는 행렬식을 규정하는 조건을 볼 때 두 개의 변수만을 포함하는 조건은 늘 적당한 \(2\)-차원 평면에서 생각할 수 있기 때문이다. 두 개의 변수를 제외한 모든 변수를 고정시키면 지금까지의 증명을 한 번에 확장할 수 있다.
예를 들어 \(3\)-차원 공간에서 생각해보자. 세 벡터 \(u, v, w\)로 생성된 평행체(그림 7), 즉 \[ t_{1}u+t_{2}v+t_{3}w,\quad 0\leq t_{i}\leq 1 \] 꼴의 모든 일차결합의 모임을 \(P(u, v, w)\)로 나타내자.
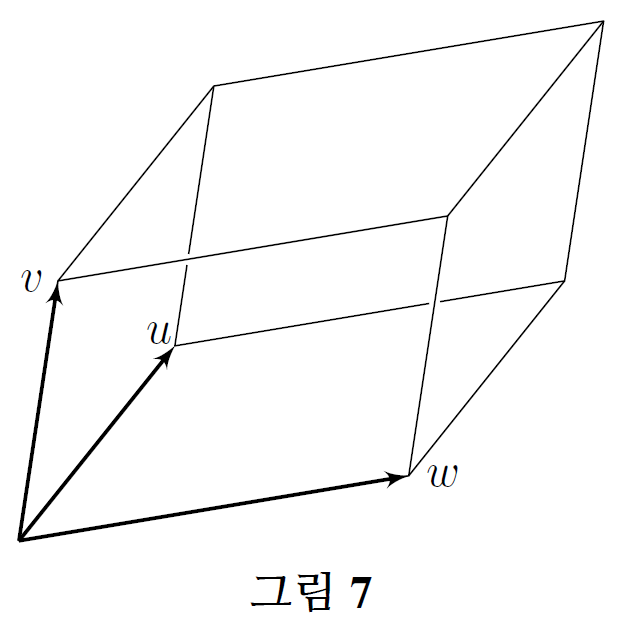
그리고 이 평행체의 체적은 \(\operatorname{Vol}(u, v, w)\)로 나타내자.
Theorem.8.
세 벡터 \(u, v, w\)로 생성된 평행체의 체적은 행렬식 \(\det(u, v, w)\)의 절댓값과 같다. 즉
\[
\operatorname{Vol}(u, v, w)=\left\vert\det(u, v, w)\right\vert
\]
이 성립한다.
이의 증명은 \(2\)-차원인 경우와 완전히 같은 방식으로 얻는다. 실제로 표준기저의 단위벡터들로 얻는 정육면체의 체적은 \(1\)이다. 만일 \(u, v, w\) 중 두 벡터가 일치한다면, 평행체 \(P(u, v, w)\)는 \(2\)-차원 평행사변형이 되어 그 (3-차원) 체적은 \(0\)임을 얻는다. 마지막으로 선형성에 관한 증명도 동일하다. 왜냐하면 선형성을 따지는 것은 하나 혹은 두 개의 변수에 관한 조건이기 때문이다. 다른 변수는 표기를 위해 사용될 뿐이지 증명 과정에서 아무 역할도 하지 않는다.
마찬가지로 \(n\)-차원 체적을 생각하고 그에 대응하는 다음의 정리를 얻을 수 있다.
Theorem.9.
벡터공간 \(\mathbb{R}^{n}\)의 \(n\)개의 벡터 \(v_{1}, \ldots, v_{n}\)에 대하여 \(v_{1}, \ldots, v_{n}\)으로 생성된 \(n\)-차원 평행체의 \(n\)-차원 체적을 \(\operatorname{Vol}(v_{1}, \ldots, v_{n})\)로 나타내자. 그러면
\[
\operatorname{Vol}(v_{1}, \ldots, v_{n})=\left\vert\det(v_{1}, \ldots, v_{n})\right\vert
\]
가 성립한다.
물론 \(v_{1}, \ldots, v_{n}\)으로 생성된 \(n\)-차원 평행체란 \[ \sum_{i=1}^{n}t_{i}v_{i},\quad 0\leq t_{i}\leq 1 \] 꼴의 일차결합을 모두 모아 놓은 집합을 일컫는다.
Remark.2. 지금까지의 증명에서 넓이가 갖는 기하학적 성질을 사용하였다. 순수하게 해석학적 관점에서 이러한 성질을 살펴볼 수 있다. 흥미가 있는 독자는 Serge Lang의 저서 [2]를 참조하여라.
Remark.3. 사실 \(2\)-차원의 경우 행렬식의 절댓값이 넓이와 일치한다는 것을 (그림 하나로) 쉽게 보일 수 있다. 그러나 이 글에서 다소 복잡해보이는 방식을 고집한 이유는 \(3\)-차원 혹은 \(n\)-차원으로의 일반화를 염두에 두었기 때문이다.
이제 정리 1을 선형사상의 관점에서 살펴보자. 평면 상의 두 벡터 \(v, w\)가 주어졌을 때, \(L(e_{1})=v\)와 \(L(e_{2})=w\)를 만족시키는 선형사상 \[ L: \mathbb{R}^{2}\to\mathbb{R}^{2} \] 가 유일하게 존재함을 알고 있다. 또한 \[ v=ae_{1}+ce_{2},\quad w=be_{1}+de_{2} \] 로 둘 때, 선형사상 \(L\)의 표준기저에 관한 행렬표현은 \[ \begin{pmatrix} a & b \\ c & d \end{pmatrix} \] 이다. 더욱이 \(e_{1}, e_{2}\)로 생성된 단위 정사각형을 \(C\)로 나타내고 \(v, w\)로 생성된 평행사변형을 \(P\)로 나타낼 때, \(P\)는 \(C\)의 \(L\)에 의한 상이다. 즉 \(L(C)=P\)이다. 이는 \(0\leq t_{i}\leq 1\)에 대하여 \[ L(t_{1}e_{1}+t_{2}e_{2})=t_{1}L(e_{1})+t_{2}L(e_{2})=t_{1}v+t_{2}w \] 로부터 확인된다. 만일 선형사상의 행렬식을 그 선형사상의 행렬표현의 행렬식으로 정의한다면 \begin{equation}\label{eq:star} (\mbox{\(P\)의 넓이})=\left\vert\det(L)\right\vert \tag{2} \end{equation} 를 얻는다.
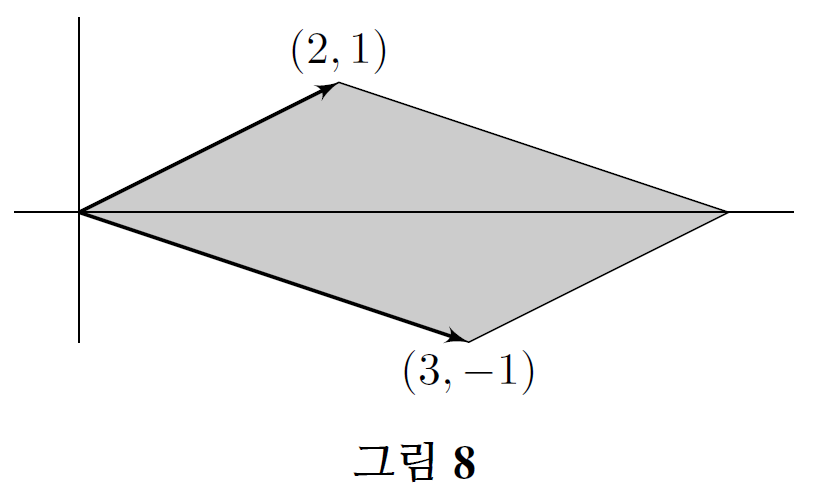
구체적으로 계산하는 예를 하나 살펴보자. 두 벡터 \((2, 1)\)과 \((3, -1)\)로 생성된 평행사변형(그림 8)의 넓이는 행렬식 \[ \begin{vmatrix} 2 & 1 \\ 3 & -1 \end{vmatrix}=-5 \] 의 절댓값, 즉 \(5\)와 같다.
Theorem.10.
두 벡터로 생성된 평행사변형 \(P\)와 선형사상 \(L: \mathbb{R}^{2}\to\mathbb{R}^{2}\)에 대하여
\[
(\mbox{\(L(P)\)의 넓이})=\left\vert\det(L)\right\vert\cdot(\mbox{\(P\)의 넓이})
\]
가 성립한다.
Proof. 평행사변형 \(P\)가 두 벡터 \(v, w\)로 생성되었다고 하자. 그러면 \(L(P)\)는 \(L(v)\)와 \(L(w)\)로 생성된다(그림 9). 조건 \[ L_{1}(e_{1})=v, \quad L_{1}(e_{2})=w \] 를 만족시키는 선형사상 \(L_{1}: \mathbb{R}^{2}\to\mathbb{R}^{2}\)가 존재한다. 표준기저로 생성된 단위 정사각형을 \(C\)로 두면 \(P=L_{1}(C)\)가 성립하며 앞서 관찰했던 \eqref{eq:star}로부터 \[ \operatorname{Vol}\left(L(P)\right)=\left\vert\det(L\circ L_{1})\right\vert=\left\vert\det(L)\det(L_{1})\right\vert=\left\vert\det(L)\right\vert\cdot\operatorname{Vol}(P) \] 를 얻는다.

Corollary.11.
좌표축과 평행한 변을 갖는 임의의 직사각형 \(R\)과 임의의 선형사상 \(L: \mathbb{R}^{2}\to\mathbb{R}^{2}\)에 대하여
\[
\operatorname{Vol}\left(L(R)\right)=\left\vert\det(L)\right\vert\cdot\operatorname{Vol}(R)
\]
이 성립한다.
Proof. 직사각형 \(R\)의 이웃한 두 변의 길이가 \(c_{1}, c_{2}\)라 하자. 그리고 \(c_{1}e_{1}\)과 \(c_{2}e_{2}\)로 생성된 직사각형을 \(R_{1}\)으로 두자. 그러면 \(R\)은 적당한 벡터 \(u\)로 \(R_{1}\)을 평행이동하여 얻은 직사각형이 된다. 이때 \[ L(R)=L(R_{1}+u)=L(R_{1})+L(u) \] 이므로 \(L(R)\)은 \(L(u)\)로 \(L(R_{1})\)을 평행이동하여 얻은 도형이다(그림 10). 평행이동은 넓이를 변화시키지 않으므로 정리 1로부터 원하는 결과를 얻는다.

연습문제
- \(v, w\)에 관한 함수 \(g(v, w)\)가 행렬식을 규정하는 세 성질 중 처음의 두 성질을 만족시킨다면 임의의 \(v, w\)에 대하여 \[ g(v, w)=-g(w, v) \] 가 성립함을 보여라.
- 다음 주어진 벡터들로 생성된 평행사변형의 넓이를 구하여라.
- \((2, 1), (-4, 5)\)
- \((3, 4), (-2, -3)\)
- 다음 주어진 점들을 세 꼭짓점으로 갖는 평행사변형의 넓이를 구하여라.
- \((1, 1), (2, -1), (4, 6)\)
- \((-3, 2), (1, 4), (-2, -7)\)
- \((2, 5), (-1, 4), (1, 2)\)
- \((1, 1), (1, 0), (2, 3)\)
- 다음 주어진 세 벡터로 생성된 평행체의 체적을 구하여라.
- \((1, 1, 3), (1, 2, -1), (1, 4, 1)\)
- \((1, -1, 4), (1, 1, 0), (-1, 2, 5)\)
- \((-1, 2, 1,), (2, 0, 1), (1, 3, 0)\)
- \((-2, 2, 1), (0, 1, 0), (-4, 3, 2)\)
참고문헌
- Lang, S. (1986). Introduction to Linear Algebra Second Edition., Springer
- Lang, S. (2013). Undergraduate analysis. Springer Science & Business Media