콘 아이스크림
\(12\)가지의 맛을 고를 수 있는 아이스크림 가게에서, 중복을 허용하지 않고 \(5\)개의 싱글 콘 아이스크림을 주문하는 경우의 수는 \(\binom{12}{5}\)임을 알고 있다. 또한 중복을 허용하여 싱글 콘 아이스크림을 주문하는 경우의 수는 \(\binom{12+5-1}{5}\)인 것도 알고 있다. 이제 하나의 콘에 두 가지 맛을 고를 수 있는 더블 콘 아이스크림을 생각해보자. 물론 콘에 아이스크림을 담는 순서를 고려해야 한다는 진정한 아이스크림 미식가와 아이스크림을 담는 순서는 고려할 필요 없다고 생각하는 사람들을 고려해야할 것이다. 한편 아이스크림을 담는 순서에 무관한 더블 콘 아이스크림의 개수를 세는 것은, 아이스크림 두 덩이리를 접시에 담은 것의 개수를 세는 것으로 볼 수 있을 것이다.- \(12\)가지의 맛을 고를 수 있는 아이스크림 가게에서 중복을 허용하여 5개의 더블 콘 아이스크림을 주문할 때, 콘에 아이스크림을 담는 순서를 고려하여 주문하는 경우의 수는?
- \(12\)가지의 맛을 고를 수 있는 아이스크림 가게에서 중복을 허용하지 않고 5개의 더블 콘 아이스크림을 주문할 때, 콘에 아이스크림을 담는 순서를 고려하여 주문하는 경우의 수는?
- \(12\)가지의 맛을 고를 수 있는 아이스크림 가게에서 중복을 허용하지 않고 5개의 더블 콘 아이스크림을 주문할 때, 콘에 아이스크림을 담는 순서는 고려하지 않고 주문하는 경우의 수는?
- \(12\)가지의 맛을 고를 수 있는 아이스크림 가게에서 중복을 허용하여 5개의 더블 콘 아이스크림을 주문할 때, 콘에 아이스크림을 담는 순서는 고려하지 않고 주문하는 경우의 수는?
최단 경로의 개수
- \(10\)개의 R과 \(6\)개의 U를 배열하는 경우의 수는? (R과 U는 각각 Right와 Up에서 따온 것이다.)
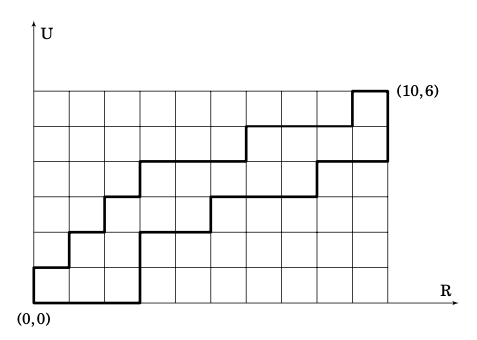
- 좌표평면에서 좌표축과 평행하며 길이가 \(1\)인 선분들을 (끝점을 제외하곤) 겹치지 않게 이어붙여 \((0, 0)\)에서 \((10, 6)\)으로 가는 경로를 만든다. 이러한 경로 중 가장 짧은 것은 몇 개인가? 그림 1은 이러한 경로 중 두 개를 예시로 나타낸 것이다.
- \(3\)개의 X, \(6\)개의 Y, \(7\)개의 Z로 이루어진 word는 총 몇 개인가?
- \(3\)-차원 좌표공간에서 좌표축과 평행하며 길이가 \(1\)인 선분들을 (끝점을 제외하곤) 겹치지 않게 이어붙여 원점에서 \((3, 6, 7)\)으로 가는 경로를 만든다. 이러한 경로 중 가장 짧은 것은 몇 개인가?
- \(x\)개의 X, \(y\)개의 Y로 이루어진 word는 총 몇 개인가?
- \(x\)와 \(y\)가 모두 음이 아닌 정수일 때, 좌표평면에서 좌표축과 평행하며 길이가 \(1\)인 선분들을 (끝점을 제외하곤) 겹치지 않게 이어붙여 \((0, 0)\)에서 \((x, y)\)로 가는 경로를 만든다. 이러한 경로 중 가장 짧은 것은 몇 개인가? 좌표축 및 제1사분면의 격자점마다 이 문제의 답을 표시하면 하나의 패턴을 발견할 수 있다. 답을 표시한 종이를 회전하여 원점을 맨 위로 오게하면 Pascal의 삼각형을 발견할 수 있을 것이다.
- \(x\)개의 X, \(y\)개의 Y, \(z\)개의 Z로 이루어진 word는 총 몇 개인가?
- \(x, y, z\)가 모두 음이 아닌 정수일 때, 좌표공간에서 좌표축과 평행하며 길이가 \(1\)인 선분들을 (끝점을 제외하곤) 겹치지 않게 이어붙여 원점에서 \((x, y, z)\)로 가는 경로를 만든다. 이러한 경로 중 가장 짧은 것은 몇 개인가?
- 그림 1에서 직사각형은 몇 개 있는가?
- 그림 1에서 정사각형은 몇 개 있는가?