1. 역사적 단상
- 갈릴레오는 (중심각이 $90^\circ$인) 원호 모양의 철사에 구슬을 꿰었을 때, 마찰없이 구슬이 미끄러지는데 걸리는 시간을 생각하였다.
 미적분의 이론을 통해 구슬의 강하시간을 계산하면
\[
\sqrt{\frac{L}{g}}\int_0^{\pi/2}\frac{1}{\sqrt{1-\sin^2\left(\frac{1}{2}\alpha\right)\sin^2\beta}}\ \mathrm{d}\beta
\]
이고, 이는 약 $1.8541\sqrt{L/g}$이다.
미적분의 이론을 통해 구슬의 강하시간을 계산하면
\[
\sqrt{\frac{L}{g}}\int_0^{\pi/2}\frac{1}{\sqrt{1-\sin^2\left(\frac{1}{2}\alpha\right)\sin^2\beta}}\ \mathrm{d}\beta
\]
이고, 이는 약 $1.8541\sqrt{L/g}$이다. - 갈릴레오는 원호를 다각선으로 근사시켰을 때의 구슬의 낙하시간은 항상 [원호를 따라 낙하하는 구슬]의 낙하시간보다 크다고 추론하였다. (자세한 내용이 참고도서 [2]의 6.1절에 소개되어있다.) 어떤 사람들은 갈릴레오가 최단강하선이 원호임을 주장했다고 하는데, 이는 역사학자들 사이에 여러 이견이 있는 듯 하다.
- 요한 베르누이는 1696년 학술지 『Acta Eruditorum』에서 ‘세계에서 가장 뛰어난 수학자들(the most brilliant mathematicians in the world)’을 향해 다음과 같은 문제를 제시하였다. (이 학술지는 1682년에 처음으로 출판된 독일 최초의 학술지이다.)
어떤 물체가 점 $\mathrm{A}$에서 출발하여 점 $\mathrm{B}$까지 중력에 의해서만 이동할 때, 소요시간을 최소화하려면 이 물체는 어떤 경로를 따라 이동해야 하는가?
이 문제에 대해, 야곱 베르누이, 라이프니츠, 로피탈 등 여러 수학자가 옳은 답을 제시하였다. 그리고 익명으로 투고된 답안도 있었다. 요한은 이 답안을 보고 “발톱 자국으로부터 그것이 사자의 것임을 알 수 있다.”라고 말했다고 한다.[5] - 베르누이의 도전은 결코 호의적이지 않았다. 그리고 베르누이는 갈릴레오의 업적은 전혀 언급하지 않았으며, 오히려 최단강하에 관해 갈릴레오의 업적은 전혀 알지 못했었다고 주장했다. 또한 베르누이는 뉴턴과 사이가 좋지 못했는데, 이 최단강하선의 풀이에 대한 찬사가, 뉴턴을 향한 거의 유일한 좋은 평가라고 한다.[2] 사실 요한 베르누이는 미적분학의 창시자가 누구인가에 대한 싸움에서 라이프니츠의 편에서서 전투적인 모습을 보였었다고 한다.[4]
2. 준비학습: 에너지 보존법칙
- 질량이 $m$인 물체가 $v=y'(t)$의 속도로 자유낙하하고 있을 때, 이 물체의 운동에너지는 \[\frac{1}{2}mv^2=\frac{1}{2}m(y'(t))^2\]으로 정의되며, 이 물체의 위치에너지는 $mgy(t)$로 정의된다. 그리고 운동에너지와 위치에너지의 합을 역학적 에너지라고 한다.
- 중력에 의해서 자유낙하하는 물체의 가속도는 $y''(t)=-g$이다. 역학적 에너지를 시간 $t$에 대하여 미분해보면 \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{1}{2}m(y'(t))^2+mgy(t)\right) &= my'(t)y''(t)+mgy'(t) \\ &= -mgy'(t)+mgy'(t)=0 \end{align*} 임을 알 수 있다. 따라서 역학적 에너지의 총량은 시간에 따라 변하지 않음을 알 수 있다.
- 중력장 안에서 $3$차원 운동을 하고 있는 질량 $m$인 물체의 시각 \(t\)에서의 위치를 \[\mathbf{X}(t)=(x(t), y(t), z(t))\]라 하면, 이 물체의 운동에너지는 \[ \frac{1}{2}m\Vert \mathbf{X}'(t)\Vert^2 \] 위치에너지는 \[ mgz(t) \] 이다. 중력에 의해서만 운동하는 이 물체의 역학적 에너지를 시간에 대해 미분해보면 \begin{align*} \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{1}{2}m\Vert \mathbf{X}'(t)\Vert^2+mgz(t)\right) & = \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{1}{2}m(\mathbf{X}'(t)\cdot \mathbf{X}'(t))+mgz(t)\right) \\[4pt] & = m (\mathbf{X}'(t)\cdot \mathbf{X}''(t))+mgz'(t) \\[8pt] & = m\left( (x'(t), y'(t), z'(t))\cdot (0, 0, -g)\right)+mgz'(t) \\[8pt] &= -mgz'(t)+mgz'(t)=0 \end{align*} 으로 역시 역학적 에너지는 시간에 따라 변하지 않음을 알 수 있다.
- 물체의 운동을 살펴볼 때, 물체가 가진 속도, 에너지 등 물리적인 정보를 해석하기 위해서는 그 물체에 작용하는 모든 힘을 고려해야한다. 지금 살펴보고 있는 운동에서는
- 마찰력이나 공기의 저항은 무시하고 있다.
- 중력의 영향을 고려하고 있다.
- 철사 혹은 미끄럼틀 같은 경로를 정해주어 물체의 이동에 영향을 주고 있다.
3. 베르누이의 풀이
스넬의 법칙을 상기해보자.
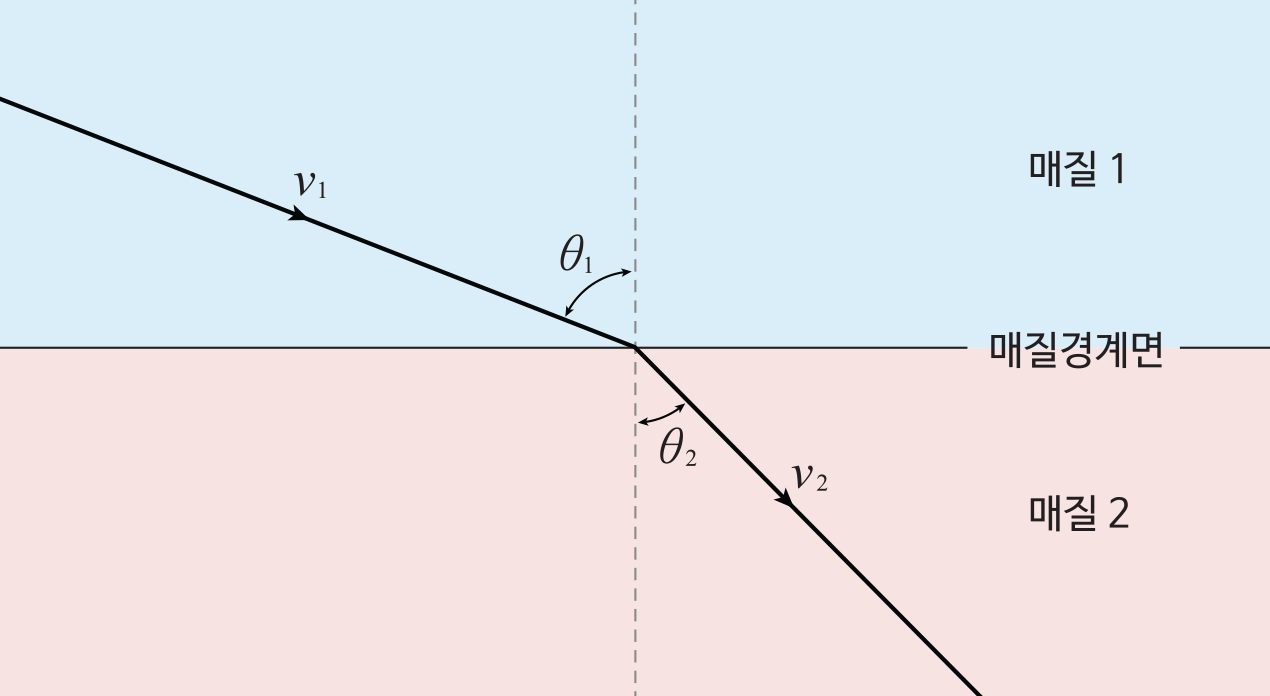
그림과 같이 서로 다른 매질1, 매질2가 있고 각각을 통과할 때의 속력이 $v_1, v_2$라고 할 때, B에서 A로 가는 빛의 경로는 \[ \frac{\sin\theta_1}{v_1}=\frac{\sin\theta_2}{v_2} \] 를 만족시킨다. 최단 강하선 문제에 대한 요한 베르누이의 풀이는 에너지 보존 법칙과 스넬의 법칙을 이용한 풀이이다.
이제 베르누이의 풀이를 살펴보자. 먼저 최단 강하선 $y=f(x)$가 있을 때, 이 곡선이 만족시켜야 하는 조건이 무엇인지 살펴보자. 편의상 $y$축의 방향을 아래쪽으로 향하게 하고(즉 $y$축의 방향을 속력이 증가하는 방향으로 두고) 점 $\mathrm{A}$를 원점에 위치시키자.
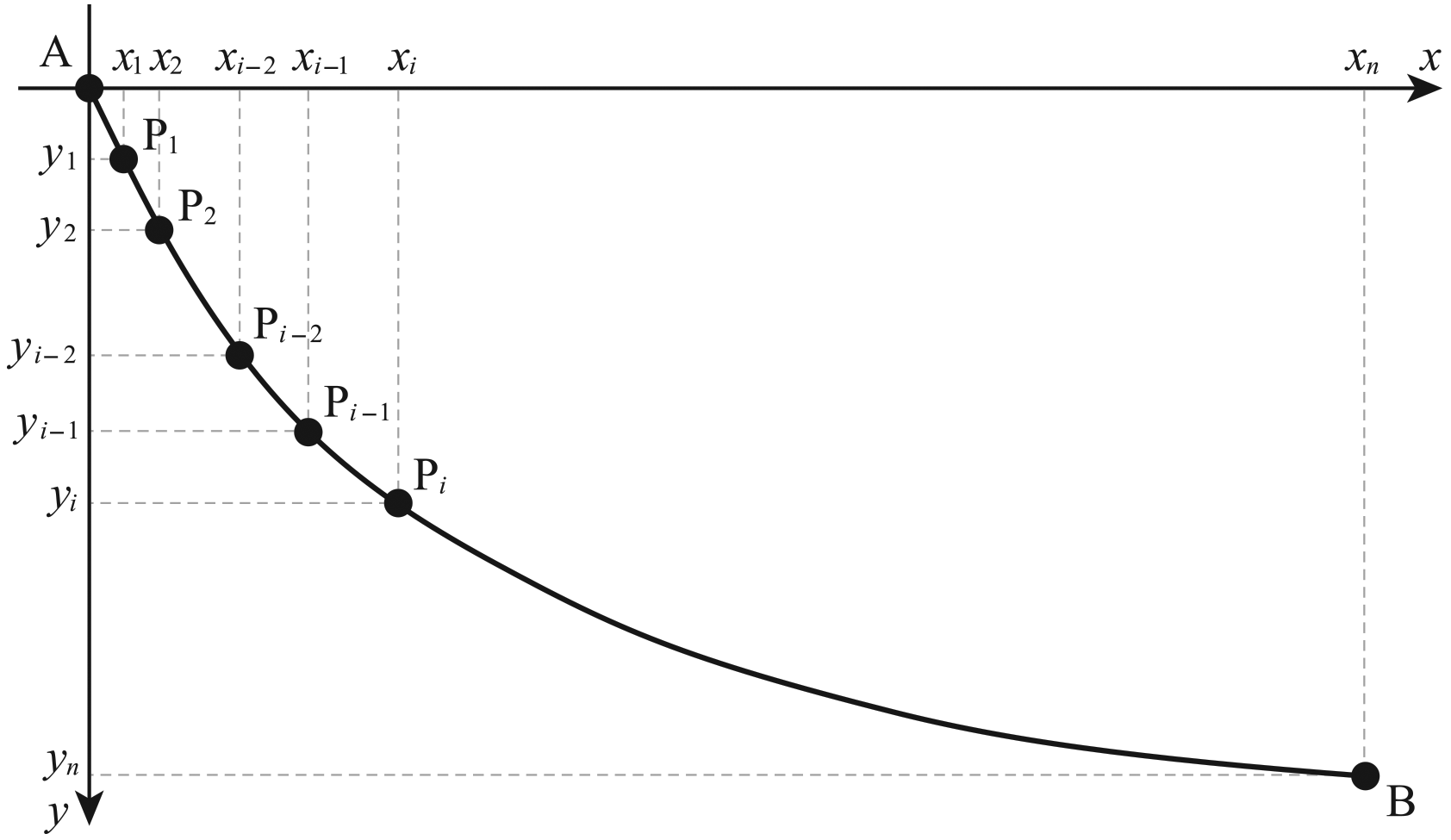
그리고 점 $\mathrm{B}$의 좌표는 $(b_1, b_2)$로 쓰자. 그림과 같이 $y$축을 $n$등분하는 가로선들을 그어, 이 가로선이 최단강하선과 만나는 점들을 $\mathrm{P}_i(x_i, y_i)$로 쓰자(단, $i=1,\,\ldots,\,n$). 물론 $\mathrm{A}=\mathrm{P}_0$, $\mathrm{B}=\mathrm{P}_n$이다.
베르누이는 그림에서 가로선들을 서로 다른 매질들의 경계면으로 생각하였다. 즉 최단강하선의 문제를 아래로 갈수록 덜 조밀한(즉 아래로 갈 수록 빛이 더 빠르게 이동할 수 있는) 여러 개의 층이 있을 때, 빛이 어떻게 이동하는가에 대한 문제를 통해 살펴본 것이다.
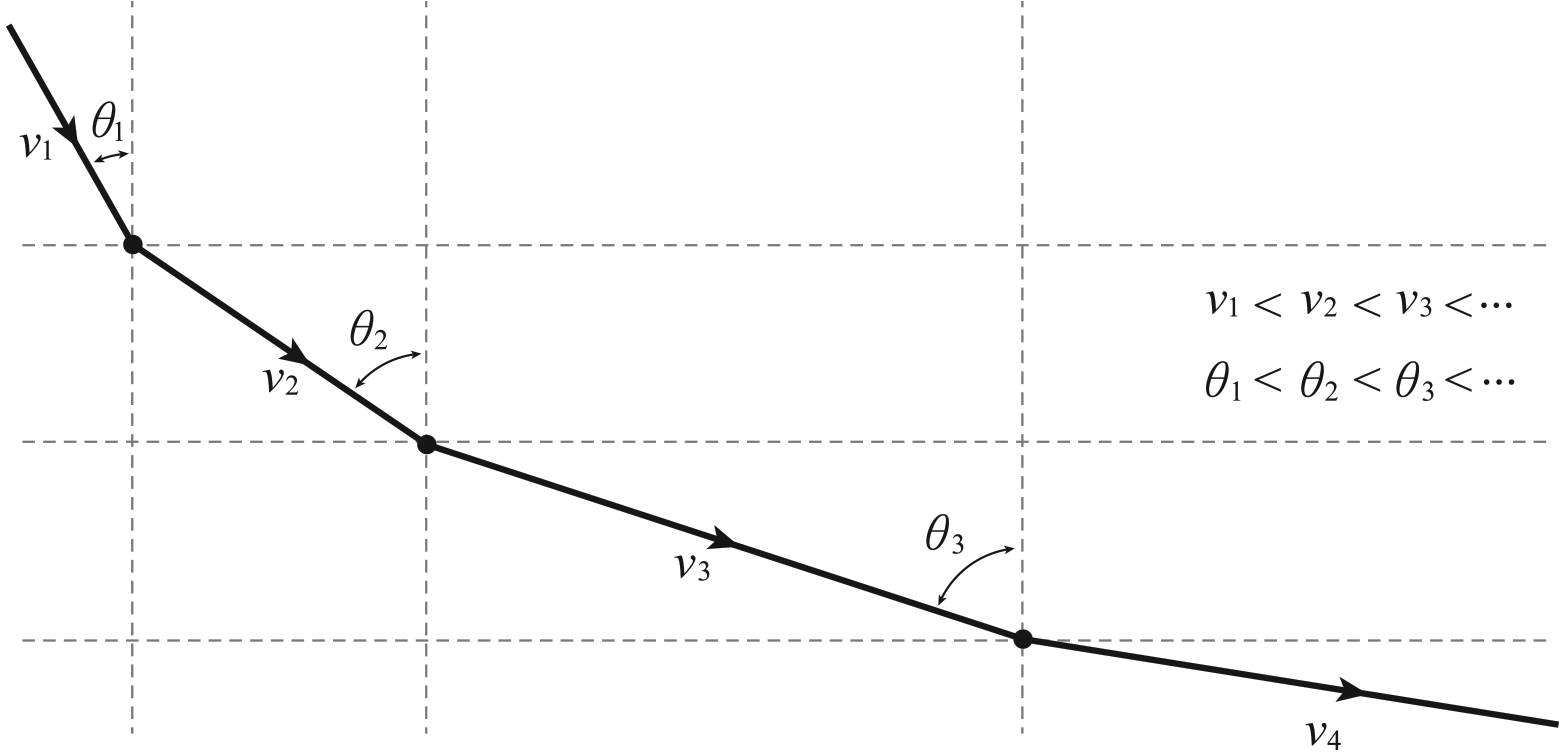
그림의 경로가 빛의 경로, 즉 소요시간을 최소화하는 경로라면, 역시 스넬의 법칙에 따라 모든 $i$에 대하여 \[ \frac{\sin\theta_{i-1}}{v_{i-1}}=\frac{\sin\theta_i}{v_i} \] 가 성립한다. 따라서 \[ \frac{\sin\theta_i}{v_i}=\mbox{(상수)} \] 로 둘 수 있다. 이제 층의 개수를 무한히 증가시키면 빛의 경로는 부드러운 곡선을 따르게 되는데, 그림과 같이 각 점에서의 속력 $v$에 대하여 등식 \begin{equation} \frac{\sin\theta}{v}=\mbox{(상수)}\tag{1} \end{equation} 가 성립한다.

이때 점 $\mathrm{P}(x, y)$에서의 속력 $v$는 에너지 보존 법칙을 이용해 구할 수 있다. 에너지 보존 법칙에 따르면, 물체가 낙하하면서 줄어든 위치 에너지만큼 그 물체가 가진 운동에너지가 증가한다. 그런데 점 $\mathrm{P}(x, y)$에서 처음에 비해 줄어든 위치에너지는 $mgy$이고 $\mathrm{P}_0$에서 이 물체가 가진 운동에너지가 $0$이었으므로 늘어난 운동 에너지는 $\frac{1}{2}mv^2$이고 이는 $mgy$와 같다. 따라서 \begin{equation} v=\sqrt{2gy}\tag{2} \end{equation} 가 성립한다. 위의 그림에서와 같이 접선이 가로선과 이루는 각을 $\alpha$라 하면, $\theta+\alpha=\pi/2$이고 따라서 \begin{align*} \sin\theta&=\cos\alpha=\frac{1}{\sec\alpha}=\frac{1}{\sqrt{1+\tan^2\alpha}} \\ & = \frac{1}{\sqrt{1+(\mathrm{d}y/\mathrm{d}x)^2})}=\frac{1}{\sqrt{1+(y')^2}} \end{align*} 이 성립한다. 이 결과와 식 (1), (2)를 이용하여 \[ (\mbox{상수})=\frac{\sin\theta}{v}=\frac{\frac{1}{\sqrt{1+(y')^2}}}{\sqrt{2gy}}=\frac{1}{\sqrt{2gy}\sqrt{1+(y')^2}} \] 을 얻는다. 이로부터 최단 강하선이 만족시키는 미분방정식 \[ y(1+(y')^2)=C\tag{3} \] 를 얻는다. (단, \(C\)는 상수.)
일반적으로 선형이 아닌 미분방정식은 해를 구하는 것이 쉽지는 않지만, 식 (3)은 변수분리형 미분방정식으로 해를 구할 수 있다. 실제로 식 (3)을 \[ \mathrm{d}x=\mathrm{d}y\sqrt{\frac{y}{C-y}} \] 로 변형하고, $\tan\varphi=\sqrt{\frac{y}{C-y}}$로 두면 \begin{align*} &\frac{y}{C-y}=\tan^2\varphi=\frac{\sin^2\varphi}{\cos^2\varphi}\\[5pt] \Rightarrow\quad & y\cos^2\varphi =C\sin^2\varphi -y\sin^2\varphi \\[8pt] \Rightarrow\quad & y=C\sin^2\varphi \end{align*} 를 얻는다. 이제 $x$를 매개변수 $\varphi$로 나타낼 수 있으면, 곡선 $y=f(x)$의 매개변수 표현을 얻는 것이 된다. 위의 마지막 식을 미분하여 $\mathrm{d}y=2C\sin\varphi\cos\varphi\ \mathrm{d}\varphi$를 얻고 이를 이용해 \begin{align*} \mathrm{d}x&=\mathrm{d}y\sqrt{\frac{y}{C-y}}=2C\sin\varphi\cos\varphi\tan\varphi\ \mathrm{d}\varphi \\[5pt] &= 2C\sin^2\varphi\ \mathrm{d}\varphi \\[8pt] &= C(1-\cos(2\varphi))\ \mathrm{d}\varphi \end{align*} 즉 $\mathrm{d}x=C(1-\cos(2\varphi))\ \mathrm{d}\varphi$를 얻고, 양변을 적분하여 \[x=\frac{1}{2} C(2\varphi-\sin(2\varphi))+C_0\] 를 얻는다. 여기서 적분상수 $C_0$는 초기조건을 통해 $0$임을 바로 알 수 있다. 이제 $2\varphi=\theta,$ $R=\frac{1}{2}C$로 두면 곡선 $y=f(x)$의 매개변수 표현 \[ x=R(\theta-\sin\theta),\quad y=%C\sin^2\varphi=\frac{1}{2}C(1-\cos(2\varphi))= R(1-\cos\theta) \] 를 얻는다. 이는 그 유명한 사이클로이드 곡선의 매개변수 표현이다.
- 상수 $R$을 적절히 조절하면, 임의의 점 $(x, y)$ (단, $x>0, y>0$)를 지나는 사이클로이드를 정할 수 있다.
- 베르누이의 풀이를 다시 살펴보면, 다음의 두 가지 가정이 중요한 역할을 하고 있음을 알 수 있다. 그리고 이 가정들은 타당하다고 생각된다.
- 곡선 $ y=f(x)$를 각 $\mathrm{P}_i$를 잇는 선분 경로들의 모임으로 근사시켜서 생각한다. ($n$이 충분히 클 때, 이는 실제 물체의 운동에 대한 좋은 근사가 된다.)
- 물체가 $\mathrm{P}_{i-1}$에서 $\mathrm{P}_i$까지 직선경로를 따르며 이동하는 속력이 $v_i$로 일정하다고 가정한다.
4. 오일러-라그랑지 방정식과 변분법
점 $\mathrm{P}_{i-1}$에서 $\mathrm{P}_i$까지 ($v_i$의 속력으로) 이동하며 걸리는 시간을 $T_{i-1}^i$라 하면, 최단강하선 문제는 \[ \lim_{n\to\infty}\sum_{i=1}^{n}T_{i-1}^i \] 를 최소화 하는 것이다. 특히 $T_{i-1}^i=\frac{\overline{\mathrm{P}_{i-1}\mathrm{P}_i}}{v_i}$이므로 위 식을 다시 쓰면 \begin{align*} \lim_{n\to\infty}\sum_{i=1}^{n}T_{i-1}^i&=\lim_{n\to\infty}\sum_{k=1}^n \frac{\sqrt{\Delta x_i^2+\Delta y_i^2}}{v_i} \\ & = \lim_{n\to\infty}\sum_{i=1}^n \frac{\sqrt{1+(\Delta y_i/\Delta x_i)^2}}{\sqrt{2gy_i}}\cdot \Delta x_i \end{align*} 이다. 즉 최단강하선 문제는 \[ \int_0^{b_1}\frac{\sqrt{1+(y')^2}}{\sqrt{2gy}} \mathrm{d}x \] 를 최소화하는 문제이다. 다시 말해,
주어진 경로에 따르는 소요시간을 재는 함수 $T$를 생각할 때, $T$가 최소가 되는 $y=f(x)$가 무엇인가?가 궁금한 것이다. 여기서 $T$는 곡선(함수)을 실수로 대응시키는 범함수이다. 이처럼 범함수의 극대, 극소(혹은 최대, 최소)를 찾는 기법을 변분법이라고 부른다.
미분가능한 함수 $f:[0, b_1]\to\mathbb{R}$와 이변수 함수 \[\mathscr{L}(u, v):=\frac{\sqrt{1+v^2}}{\sqrt{2gu}}\]를 생각할 때, 이를 이용하여 얻은 범함수 \[ T(f)=\int_0^{b_1}\mathscr{L}(f(x), f'(x)) \mathrm{d}x% =\int_0^{b_1}\frac{\sqrt{1+(f'(x))^2}}{\sqrt{2gf(x)}} \mathrm{d}x \] 의 최솟값을 생각하는 것이 바로 최단강하선 문제이다.
$T$는 함수들의 집합 $\mathscr{F}=\{ f\in C^\infty[0, b_1]\mid f(0)=0, f(b_1)=b_2\} $에서 정의된 범함수이다. 만일 $f$가 $T$를 최소가 되게 하는 함수라면, 임계점 정리에 의해, 임의의 함수 \[ h:[0, b_1]\to \mathbb{R},\quad h(0)=0, h(b_1)=0 \] 에 대하여, \[ g(t):=\int_0^{b_1}\mathscr{L}(f(x)+th(x), f'(x)+th'(x)) \mathrm{d}x \] 는 $t=0$에서 최솟값을 갖는다. 따라서 \begin{align*} 0=g'(0)&= \frac{\mathrm{d}}{\mathrm{d}t}\Big\vert_{t=0} \int_0^{b_1}\mathscr{L}(f(x)+th(x), f'(x)+th'(x)) \mathrm{d}x \\ &= \int_0^{b_1} \frac{\mathrm{d}}{\mathrm{d}t}\Big\vert_{t=0} \mathscr{L}(f(x)+th(x), f'(x)+th'(x)) \mathrm{d}x \\ &= \int_0^{b_1} \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x) )\cdot h(x)+\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))\cdot h'(x)\ \mathrm{d}x \\ &= \int_0^{b_1}\left( \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x))-\frac{\mathrm{d}}{\mathrm{d} x}\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))\right)h(x)\ \mathrm{d}x \end{align*} 가 성립한다. 여기서 가장 마지막 줄의 등호는 부분적분 및 $h(b_1)=h(0)=0$을 이용하여 얻은 등식 \begin{align*} \int_a^{b_1}\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))h'(x)\mathrm{d}x &= \left.\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))h(x)\right\vert_0^{b_1}\\ &\qquad\qquad - \int_a^{b_1} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))h(x)\mathrm{d}x \\ &= - \int_a^{b_1} \frac{\mathrm{d}}{\mathrm{d}x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))h(x)\mathrm{d}x \end{align*} 를 사용하였다. 이때 $h$는 임의의 함수이므로 방정식 \begin{equation} \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x))=\frac{\mathrm{d}}{\mathrm{d} x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))\tag{4} \end{equation} 를 얻는다. $T$의 극값이 되는 함수 $y=f(x)$는 방정식 (4)를 만족시켜야 한다. 방정식 (4)를 오일러-라그랑지 방정식이라 부른다.
오일러-라그랑지 방정식의 양변에 $f'(x)$를 곱하면 \[ f'(x) \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x))=f'(x) \frac{\mathrm{d}}{\mathrm{d} x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x)) \] 이고, 이 식에 다시 $f''(x)\frac{\mathrm{\partial}}{\partial v}\mathscr{L}(f(x), f'(x))$를 더하여 \begin{align*} f'(x) \frac{\partial}{\partial u}\mathscr{L}(f(x), f'(x)) +& f''(x)\frac{\mathrm{\partial}}{\partial v}\mathscr{L}(f(x), f'(x)) \\ &=f'(x) \frac{\mathrm{d}}{\mathrm{d} x} \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))+f''(x)\frac{\mathrm{\partial}}{\partial v}\mathscr{L}(f(x), f'(x)) \end{align*} 를 얻는데, 이를 다시 쓰면 \[ \frac{\mathrm{d}}{\mathrm{d}x}\mathscr{L}(f(x), f'(x))=\frac{\mathrm{d}}{\mathrm{d}x}\left( f'(x) \frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))\right) \] 이다. 따라서 \begin{equation} \mathscr{L}(f(x), f'(x))=f'(x)\frac{\partial}{\partial v}\mathscr{L}(f(x), f'(x))+C\tag{5} \end{equation} 를 얻는다. 특히 $\mathscr{L}(u, v)=\frac{\sqrt{1+v^2}}{\sqrt{2gu}}$이므로 $\frac{\partial}{\partial v}\mathscr{L}(u, v)=\frac{v}{\sqrt{2gu}\sqrt{1+v^2}}$이고 이를 식 (5)에 대입하여 \[ \frac{\sqrt{1+(f'(x))^2}}{\sqrt{2gf(x)}}=f'(x)\cdot \frac{f'(x)}{\sqrt{2gf(x)}\sqrt{1+(f'(x))^2}}+C \] 를 얻는다. 이 식을 정리하면 베르누이의 풀이에서 얻은 것과 동일한 미분방정식인 \[ y(1+(y')^2)=\text{Const.} \] 를 얻는다.
참고한 글
- 윤종국, 현대기하학 강의록(최소 하강선과 변분법)
- Paul J. Nahin, When Least is Best, Princeton University Press, (2004) / 번역서: 최상의최소(경문사/권오남 외)
- 김홍종, 미적분학2+, 서울대학교 출판부, (2017)
- William Dunham, The Calculus Gallery, Princeton University Press, (2005) / 번역서: 미적분학 갤러리(청문각/권혜승)
- Wikipedia, https://en.wikipedia.org/wiki/Brachistochrone_curve
본문의 그림들에 대하여
이 글에 있는 모든 그림은 Sooji Shin님이 직접 그려주신 그림입니다. Sooji Shin님 감사합니다.