\(
\newcommand{\rbinom}[2]{\left\langle\!{{#1}\atop{#2}}\!\right\rangle}
\newcommand{\secondstirlingnum}[2]{\left\{\!{{#1}\atop{#2}}\!\right\}}
\newcommand{\firststirlingnum}[2]{\left[\!{{#1}\atop{#2}}\!\right]}
\)

표 1: \(r\)개의 공을 \(n\)개에 상자에 빈 상자가 없도록 담기
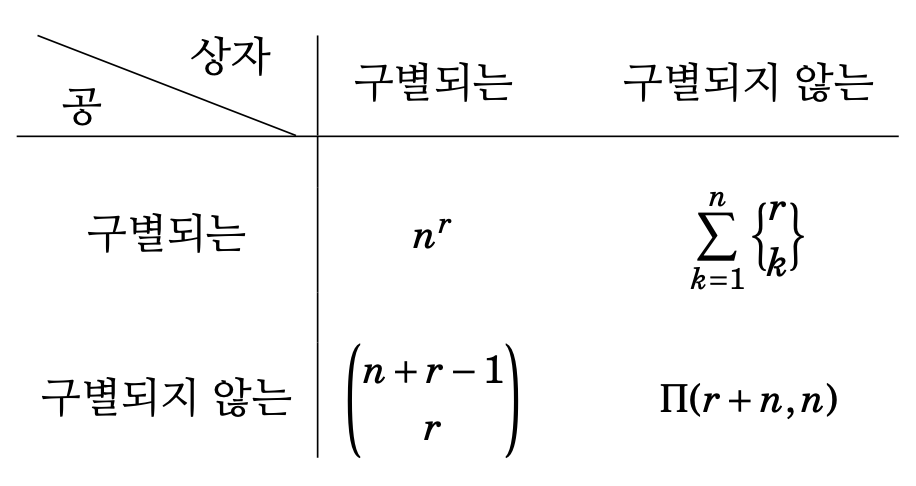
표 2: \(r\)개의 공을 \(n\)개에 상자에 담기
상자에 공을 담는 문제를 살펴보자 해보자. 여기서는 \(8\)가지의 경우를 살펴볼 것이다. 즉 공의 구별 여부, 상자의 구별 여부, 그리고 비어 있는 상자의 가능 여부에 따른 셈하기를 살펴볼 것이다.
- 구별되지 않는 \(r\)개의 공을 구별되지 않는 \(n\)개의 상자에 담을 때, 빈상자가 없도록 담는 경우의 수는?
\(\rightsquigarrow\) 이는 어떤 의미에서는 쉽다고 말 할 수 있겠으나, 이를 쉽다고 여길 수 있는 이유는 아마도 앞선 절에서 이 문제를 다루었기 때문이다. 현재 할 수 있는 가장 좋은 답은 \(\Pi(r, n)\)이다. - 구별되지 않는 \(r\)개의 공을 구별되지 않는 \(n\)개의 상자에 담는 경우의 수는?
\(\rightsquigarrow\) 이번에도 \(n\)개의 공을 추가하여 생각하면, \(\Pi(r+n, n)\)가 찾는 답임을 알 수 있다. - 구별되지 않는 \(r\)개의 공을 서로 구별되는 \(n\)개의 상자에 담는 경우의 수는?
\(\rightsquigarrow\) 이 문제의 답이 \(\rbinom{n}{r}\)임을 잘 알고 있다. - 구별되지 않는 \(r\)개의 공을 서로 구별되는 \(n\)개의 상자에 담을 때, 빈상자가 없도록 담는 경우의 수는?
\(\rightsquigarrow\) 이 문제의 답이 \(\rbinom{n}{r-n}\)임을 알고 있으며, 이는 \(\binom{r-1}{n-1}\)과 같다. - 서로 구별되는 \(r\)개의 공을 서로 구별되는 \(n\)개의 상자에 담는 경우의 수는?
\(\rightsquigarrow\) 거의 중학교 문제라 할 수 있는 이 문제의 답은 \(n^{r}\)이다. - 서로 구별되는 \(r\)개의 공을 서로 구별되는 \(n\)개의 상자에 담을 때, 빈상자가 없도록 담는 경우의 수는?
\(\rightsquigarrow\) 서로 구별되는 \(r\)개의 공을 서로 구별되는 \(n\)개의 상자에 담은 경우 중에 \(i\)번째 상자가 비어 있게 들어가 있는 경우들을 모아 놓은 것을 \(A_{i}\)로 나타내자. 어느 \(A_{1}, A_{2}, \ldots, A_{n}\)에도 들어 있지 않은 경우를 세기 위해 PIE의 보조정리를 활용하면 \[ \sum_{k=0}^{n}(-1)^{k}\binom{n}{k}(n-k)^{r} \] 를 얻는다. (미적분학의 급수 이론을 공부해 본 학생은 \((e^{x}-1)^{n}\)를 이항정리를 활용하여 \(x\)의 거듭제곱급수로 전개할 수 있을 것이다. 그 거듭제곱급수의 \(x^{r}/r!\)의 계수를 생각해보라.) - 서로 구별되는 \(r\)개의 공을 구별되지 않는 \(n\)개의 상자에 담을 때, 빈상자가 없도록 담는 경우의 수는?
\(\rightsquigarrow\) 어떤 상자 안에 공이 하나라도 담기면, 그 상자는 담고 있는 공 때문에 다른 상자들과 구별되게 된다. (오오오! 고것 참 산뜻한 트릭이군!) 따라서 바로 위에서 구한 답에 \(n!\)를 나누어 줌으로써, 이 문제의 답인 \[ \frac{1}{n!}\sum_{k=0}^{n}(-1)^{k}\binom{n}{k}(n-k)^{r} \] 를 얻는다. 이 식이 나타내는 수를 \(\secondstirlingnum{r}{n}\)로 나타내며 이를 제2종 Stirling수(Stirling number of the second kind)라 부른다. \(\secondstirlingnum{r}{1}=\secondstirlingnum{r}{r}=1\)이 성립하며, \(1 < n < r\)일 때, \[ \secondstirlingnum{r}{n}=\secondstirlingnum{r-1}{n-1}+n\secondstirlingnum{r-1}{n} \] 이 성립함을 알 수 있다. 바로 위의 등식은 \(r\)번째 공이 한 상자에 자신만 들어 있는 경우와 그렇지 않은 경우를 생각하여 얻을 수 있다. 이 점화관계를 이용하면 제2종 Stirling수에 관한 표를 만들거나 특정한 값을 계산할 수 있을 것이다.
제1종 Stirling수(Stirling number of the first kind)에 관하여 언급하고자 잠시 옆길로 샌다. Striling수 \(\secondstirlingnum{r}{n}\)은 원소가 \(r\)개인 집합을 공집합이 아닌 부분집합 \(n\)개로 분할하는 경우의 수를 세는 것이다. 제1종 Striling수 \(\firststirlingnum{r}{n}\)은 원소가 \(r\)개인 집합을 공집합이 아닌 부분집합 \(n\)개로 분할한 후, 각 부분(부분집합)들의 원소를 원형으로 배열하는 경우의 수를 세는 것이다. 즉 \(r\)명의 사람을 \(n\)개의 구별되지 않는 원탁에 앉힐 때, 빈 원탁이 없도록 앉히는 경우의 수가 곧 \(\firststirlingnum{r}{n}\)이다. 보통 “\(\secondstirlingnum{r}{n}\)”를 “\(r\) subset \(n\)”으로 읽고, “\(\firststirlingnum{r}{n}\)”는 “\(r\) cycle \(n\)”으로 읽는다. \(\firststirlingnum{r}{1}=(n-1)!\)과 \(\firststirlingnum{r}{r}=1\)이 성립하며, \(1 < n < r\)일 때, \[ \firststirlingnum{r}{n}=\firststirlingnum{r-1}{n-1}+(r-1)\firststirlingnum{r-1}{n} \] 이 성립함을 알 수 있다. 바로 위의 등식은 Lucky Pierre가 한 원탁에 홀로 앉은 경우와 그렇지 않은 경우를 생각하여 얻을 수 있다. (그렇지 않은 경우에 그는 \(r-1\)명의 사람 중 한 명의 오른쪽 자리에 앉을 수 있다.) - 서로 구별되는 \(r\)개의 공을 구별되지 않는 \(n\)개의 상자에 담는 경우의 수는?
\(\rightsquigarrow\) 현재 할 수 있는 가장 좋은 답변은, 적어도 \(1\)개의 공을 담고 있는 상자의 개수에 관한 모든 경우를 고려하는 것이다. 즉 이 문제의 답은 \[ \sum_{k=1}^{n}\secondstirlingnum{r}{k} \] 이다.
지금까지의 관찰을 두 개의 표로 정리하였다. 문제 \(6, 7, 4, 1\)번의 결과는 표 1에, 문제 \(5, 8, 3, 2\)번의 결과는 표 2에 정리되어 있다.


Optional Problem.
사람 \(6\)명을 \(3\)개의 구별되지 않는 원탁에 앉힐 때,
- 비어 있는 원탁이 없도록 앉히는 경우의 수는?
- 비어 있는 원탁이 있을 수 있을 때의 경우의 수는?