Introduction to Algebraic Topology #2
Scribed by Yeohyeon Lee
2.2 Connected Componoents
- 위상공간 \( (X, \mathscr{T})\)의 부분공간 \(A\)가 disconnected라는 것은 \[ \exists U, V\in\mathscr{T}\setminus\{\varnothing\}\quad \mbox{s.t.}\quad [ U\cap V=\varnothing, A\subset (U\cap A)\cup (V\cap A) ] \] 라는 뜻이다. 그리고 \(A\)가 connected라는 것은 \(A\)가 disconnected가 아니라는 뜻이다.
연결집합에 대하여 다음이 성립한다.
Theorem 2.1
- 함수 \(f : X\to Y\)이 연속이고 \(X\)가 connected이면 \(f(X)\)도 connected이다.
- \(X\)의 부분공간 \(A\)가 connected이면 \(\overline{A}\)도 connected이다.
- Let \(J\) be an arbitrary index set and $X_\alpha$ be connected for all $\alpha\in J$. If \(X=\bigcup_{\alpha\in J}X_{\alpha}\) and \(X_{\alpha}\cap X_{\beta}\neq\varnothing\) for all \(\alpha, \beta\in J\), then \(X\) is connected.
- The connected subsets of $\mathbb{R}$ are the intervals.
Proof.
- Elementary.
- (Contrapositive) \(\overline{A}\)가 disconnected라 가정하여 \(\overline{A}=U\amalg V\)를 만족시키는 공집합이 아닌 두 열린집합 \(U, V\)를 잡자. 등식 \(\overline{A}=A\cup A'\)를 생각하면 \(A\subset \overline{A}\)이고 이는 \(A\)가 \(U\)와 \(V\) 중 단 하나에 완전히 포함되어야 함을 뜻한다. 왜냐하면 예를 들어 \(A\not\subset U\)라면, \(U\)에 속하지 않는 \(A\)의 원소가 반드시 존재하고 그 원소는 \(V\)에 속해야 하므로 \(V\)는 공집합이 아니다. 따라서 \(U, V\)가 \(A\)가 disconnected임을 보이게 되는 두 열린집합이 되어 $A$가 connected라는 것에 모순이기 때문이다.
- \(X\)의 두 열린집합 \(U, V\)가 \(X\subset U\cup V\)와 \(U \cap V=\varnothing\)를 만족시킨다고 하자. 이때 $\bigcup_\alpha X_\alpha \subset U$ 혹은 $\bigcup_\alpha X_\alpha\subset V$ 중 하나만 성립해야 한다. 이를 보이자. 우선 $X_{\alpha_0} \cap U\neq \varnothing,\ X_{\alpha_0} \cap V\neq \varnothing$인 $X_{\alpha_0}$가 있다면, $U, V$는 $X_{\alpha_0}$가 disconnected인 것을 보이는 두 열린집합이 되기 때문에 모순이다. 즉 $U$의 원소도 있고 $V$의 원소도 있는 $X_\alpha$는 존재하지 않는다. 따라서 각 $\alpha\in J$에 대하여 $X_\alpha$는 $U$ 혹은 $V$의 부분집합이다. 또한 $X_{\alpha_1}\subset U,\ X_{\alpha_2}\subset V$를 만족시키는 $\alpha_1, \alpha_2$가 있다고 하면 처음의 가정에 의해 $x_0\in X_{\alpha_1}\cap X_{\alpha_2}$인 $x_0$를 잡을 수 있는데 이는 $x_0\in U\cap V$를 뜻하게 되어 $U\cap V=\varnothing$인 것에 모순이다. 따라서 $\bigcup_\alpha X_\alpha \subset U$ 혹은 $\bigcup_\alpha X_\alpha\subset V$ 중 하나만 성립한다. 이는 $U$와 $V$ 중 하나는 반드시 공집합임을 뜻한다.
- 기초해석학 참고.
- $X$가 위상공간이고 $A\subset X$일 때, $A$가 connected component라는 것은 $A$가 두 가지 조건
- $A$ is connected.
- $A$ is not contained in any larger connected subset of $X$.
- $A$가 연결성분이면 $A=\overline{A}$가 성립한다. 즉 연결성분은 닫힌집합이다.
- 두 부분공간 $X_\alpha, X_\beta$가 서로 다른 두 연결성분이면 $X_\alpha\cap X_\beta=\varnothing$이 성립한다. 이는 앞의 정리 2.1의 (iii)을 생각하면 당연하다.
- 위의 두 명제를 생각해보면 위상공간 $X$는 연결성분들의 disjoint union으로 나타낼 수 있음을 알 수 있다.
- 위상공간 \(X\)의 한 점 \(x\)에 대하여 \(x\)를 원소로 갖는 모든 연결부분집합들의 합집합은 하나의 연결성분이 되는데 이 연결성분을 connected component of \(x\) in \(X\)라 부른다.
- \(X\)가 위상공간이고 \(A\subset X\)일 때, \(A\)가 locally connected라는 것은 \(A\)의 임의의 점 \(p\)와 \(p\)의 임의의 근방 \(V\)에 대하여 \(p\in U\subset V\)를 만족시키는 열린 연결집합 \(U\)가 존재한다는 뜻이다.
Theorem 2.2 \(X\)가 locally connected이면 \(X\)의 임의의 연결성분은 open이다.
Proof. \(X_{\alpha}\)가 \(X\)의 한 연결성분이라 하자. \(X\)가 locally connected이므로 \(p\in U\)인 열린 연결집합 \(U\)가 존재한다. 만약 \(U\setminus X_{\alpha}\)의 원소가 존재한다면, \(X_{\alpha}\cup U\)는 \(X_{\alpha}\)를 진부분집합으로 갖는 연결집합이 되므로 \(X_{\alpha}\)가 연결성분이라는 것에 모순이다. 따라서 \(U\subset X_{\alpha}\)가 성립한다.
- \(X\)가 위상공간이고 \(A\subset X\)일 때, \(A\)가 path-connected라는 것은 \(A\)의 임의의 두 점 \(p, q\)에 대하여 \[ \gamma : [a, b]\to A, \mbox{where \(\gamma(a)=p, \gamma(b)=q\)} \] 를 만족시키는 연속함수 \(\gamma\)가 존재하는 것이다.
- \(X\)가 위상공간이고 \(A\subset X\)일 때, \(A\)가 locally path-connected라는 것은 \(A\)의 임의의 점 \(p\)와 \(p\)의 임의의 근방 \(V\)에 대하여 \(p\in U\subset V\)인 열린 path-connected subset \(U\)가 존재하는 것이다.
Theorem 2.3
- \(A\)가 path-connected이면 \(A\)는 connected이다.
- \(A\)가 connected and locally path-connected이면 \(A\)는 path connected이다.
Proof.
- \(A\)가 disconnected라면 \(A\subset U\amalg V,\ \exists p\in U\cap A,\ \exists q\in V\cap A\)를 만족시키는 두 열린집합 \(U, V\)와 두 점 \(p, q\)를 잡을 수 있다. \(A\)가 path-connected이므로 \(\gamma(a)=p, \gamma(b)=q\)를 만족시키는 연속함수 \(\gamma : [a, b]\to A\)가 존재한다. 이때 \(\gamma([a, b])\subset A\subset U\amalg V\)이고 특히 \[ [a, b] = \gamma^{-1}(U\cap A)\amalg \gamma^{-1}(V\cap B),\quad \gamma^{-1}(U\cap A)\neq \varnothing,\quad \gamma^{-1}(V\cap A)\neq \varnothing \] 이 성립한다. 여기서 \(\gamma\)가 연속함수이기 때문에 \(\gamma^{-1}(U\cap A),\ \gamma^{-1}(V\cap A)\)는 모두 열린집합이고 이는 \([a, b]\)가 연결집합이라는 것에 모순이다.
- 집합 \(A\)의 임의의 점 \(p\)기 주어졌다고 하자. 점 \(p\)가 \(A\)의 모든 점과 path로 연결된다는 것을 보이면 된다. 이제 집합 \(A^{*}\)를
\[
A^{*}:=\{ x\in A\mid \mbox{\(x\)는 \(p\)와 path로 연결가능}\}
\]
으로 정의하면 \(A^{*}\neq\varnothing\)이다. 왜냐하면 \(A^{*}\)는 적어도 \(p\)를 원소로 갖기 때문이다. 이제 \(A^{*}\)가 open임을 보이자. 임의의 \(q\in A^{*}\)에 대하여 \(q\)는 locally path-connected인 \(A\)의 점이므로 \(q\in W\subset A\)인 open path-connected set \(W\)가 존재한다. 여기서 \(W\subset A^{*}\)만 보이면 \(A^{*}\)가 open이라는 것을 보이게 되는 것인데 이는 거의 자명하다. 임의의 \(r\in W\)에 대하여 \(q\)에서 \(r\)까지 이어지는 path가 존재한다. 또한 \(q\in A^{*}\)이므로 \(p\)에서 \(q\)까지 이어지는 path도 존재하는데, 이들 두 path를 연결한 것도 하나의 path가 되므로 결국 \(r\)은 \(p\)와 path로 연결가능한 점이다. 즉 \(r\in A^{*}\)이므로 \(W\subset A^{*}\)이다. 다시 말해 \(A^{*}\)는 open이다.
비슷한 방법으로 \((A^{*})^{C}\)가 open임을 보일 수 있다. \(A^{*}\)와 \((A^{*})^{C}\)가 모두 공집합이 아닌 open set 이라면 \(A\)가 connected라는 것에 모순이므로 결국 \((A^{*})^{C}=\varnothing\)이어야한다. 따라서 \(A\)의 점들 중 \(p\)와 path로 연결할 수 없는 점은 존재하지 않는다.
보통위상공간 \(\mathbb{R}^{n}\)은 locally path-connected이므로 다음 따름정리를 얻는다. 직접 증명도 \(\varepsilon\)-ball을 생각하면 매우 쉽다.
Corollary 2.4 \(\mathbb{R}^{n}\)의 열린 부분집합 \(U\)에 대하여 \(U\)가 connected일 필요충분조건은 \(U\)가 path-connected인 것이다.
2.3 Patching
Theorem 3.1 [Pasting Lemma] \(X\)가 위상공간이고 \(X=A\cup B\)라 하자. 또한 \(A, B\)가 모두 open(혹은 모두 closed)이고 두 함수 $f : A\to Y,\ g : B\to Y$가 모두 연속이라 하자. 만일 모든 \(x\in A\cap B\)에 대하여 \(f(x)=g(x)\)가 성립하면, \(f\)와 \(g\)를 이용하여 \[ h(x)=\begin{cases} f(x) & \mbox{if \(x\in A\)} \\ g(x) & \mbox{if \(x\in B\)} \end{cases} \] 로 정의한 함수 \(h : X\to Y\)는 연속함수이다.
Proof. 함수 \(h\)가 잘 정의되는 것은 \(f(x)=g(x),\ \forall x\in A\cap B\)라는 조건때문에 자명하다. 먼저 \(A, B\)가 모두 open이라 가정하자. 기초적인 집합론의 이론을 이용하여 \[ \forall U\subset Y,\quad h^{-1}(U)=f^{-1}(U)\cup g^{-1}(U) \] 가 성립함을 확인할 수 있다. 이때 \(U\)가 \(Y\)의 열린부분집합이라면 \(f^{-1}(U)\)는 \(A\)에서 open이고, \(g^{-1}(U)\)는 \(B\)에서 open이므로 subspace topology의 정의에 의해 \[ f^{-1}(U)=A\cap U_{1},\quad g^{-1}(U)=B\cap U_{2} \] 인 \(X\)의 open sets \(U_{1}, U_{2}\)가 존재한다. 즉 \[ h^{-1}(U)=f^{-1}(U)\cup g^{-1}(U)=(A\cap U_{1})\cup (B\cap U_{2}) \] 이다. 이때 \(A, B\)가 모두 open이므로 \(h^{-1}(U)\)도 open이다. 한편 \(A, B\)가 모두 closed인 경우의 증명은 앞의 증명에서 \(U\)가 \(Y\)의 임의의 부분집합으로 바꾼 것과 같다.
Remark. 위상공간 \(X\)의 부분공간 \(A\)가 \(X\)의 열린 부분공간일 때, \(U\)가 \(A\)에서 열린부분집합이면 \(U\)는 \(X\)에서도 열린집합이다. 또한 \(B\)가 \(X\)의 닫힌 부분공간일 때, \(V\)가 \(B\)에서 닫혀있는 집합이라면 \(V\)는 \(X\)에서도 닫힌집합이다. 이 사실을 이용하면 위의 증명을 좀 더 간결하게 할 수 있다.
Pasting lemma는 연속함수를 만드는 방법을 이야기 하는 것이다. 이 보조정리를 살펴본 김에 James R.\ Munkres 교수의 위상수학 교재에 앞부분에 정리해 둔 연속함수를 만드는 방법에 대한 이야기를 다시 복습해보자.Theorem 3.2 [Rules for constructing continuous functions] Let $X, Y$ and $Z$ be topological spaces.
- (Constant function) If \(f : X\to Y\) maps all of \(X\) into the single point \(y_{0}\) of \(Y\), then \(f\) is continuous.
- (Inclusion) If \(A\) is a subspace of \(X\), the inclusion function \(j : A\to X\) is continuous.
- (Composites) If \(f : X\to Y\) and \(g : Y\to Z\) are continuous, then the map \(g\circ f : X\to Z\) is continuous.
- (Restricting the domain) If \(f : X\to Y\) is continuous, and if \(A\) is a subspace of \(X\), then the restricted function \(f\vert_{A} : A\to Y\) is continuous.
- (Restricting or expanding the range) Let \(f : X\to Y\) be continuous. If \(Z\) is a subspace of \(Y\) containing the image set \(f(X)\), then the function \(g : X\to Z\) obtained by restricting the range of \(f\) is continuous. If \(Z\) is a space having \(Y\) as a subspace, then the function \(h : X\to Z\) obtained by expanding the range of \(f\) is continuous.
- (Local formulation of continuity) The map \(f : X\to Y\) is continuous if \(X\) can be written as the union of open sets \(U_{\alpha}\) such that \(f\vert_{U_{\alpha}}\) is continuous for each \(\alpha\).
Proof. 이것의 증명은 추후에 쓰자.
- \(X\)가 공집합이 아닌 집합이라하고 \(\sim\)는 \(X\)에서의 한 이항관계, 즉 \(\sim\subset X\times X\)라 하자. 관계 \(\sim\)가 equivalence relation on \(X\)라는 것은 \(\sim\)가 세 조건
- \(\forall x\in X,\ x\sim x\quad\)
- \(\forall x, y\in X,\ [ x\sim y \Rightarrow y\sim x ]\quad\)
- \(\forall x, y, z\in X,\ [ x\sim y, y\sim z \Rightarrow x\sim z ]\quad \)
- 집합 \(X\!/\!_{\sim}\) 위에 상위상(quotient topology)를 정의해보자. \(\pi(x)=[x]\)로 정의된 \(X\)에서 \(X\!/\!_{\sim}\)로 가는 자연스러운 전사함수 \(\pi : X\to X\!/\!_{\sim}\)를 생각할 수 있다. 이 함수 \(\pi\)가 연속이 되도록하는 \(X\!/\!_{\sim}\) 위의 가장 섬세한 위상이 바로 \(X\!/\!_{\sim}\) 위의 상위상이다. 상위상이 주어진 위상공간 \(X\!/\!_{\sim}\)를 상공간이라 부른다. 상위상을 좀 더 구체적으로 묘사하자면, \[ \mbox{\(U \subset X\!/\!_{\sim}\) is open in \(X\!/\!_{\sim}\)}\quad \Leftrightarrow\quad \mbox{$\pi^{-1}(U)$ is open in \(X\)} \] 로 열린집합을 정의한 것이다. 앞으로 위상공간 위의 동치관계를 이용하여 만든 동치류들의 모임에서는 별다른 언급이 없어도 늘 상위상을 생각하는 것으로 약속한다.
Remark. 어떤 위상공간 위에 동치관계 혹은 분할이 주어졌을 때, 자연스러운 전사함수 \(\pi\)를 생각하여 위와 같이 상공간을 정의하였다. 책에 따라서는 정의역이 위상공간인 임의의 전사함수 \(p\)가 주어졌을 때, 그 \(p\)가 연속이 되도록하는 가장 섬세한 위상을 공역에 준 것을 \(p\)로부터 얻은 상위상이라고 부르기도 한다.
Theorem 3.3 함수 \(f : Y\to Z\)가 연속함수라 하자. \(Y\) 위에 관계 \(\sim\)를 \(y_{1}\sim y_{2}\ \Leftrightarrow\ f(y_{1})=f(y_{2})\)로 정의하면 $\sim$은 잘 정의된 동치관계이며 \(f=\overline{f}\circ\pi\)인 연속함수 $\overline{f} : Y\!/\!_{\sim}\to Z$가 존재한다.
Proof. 이 정리의 요지는 아래 diagram에서 보여주는 방식으로 상공간 \(Y\!/\!_{\sim}\) 위에 연속함수를 만들 수 있다는 것이다.
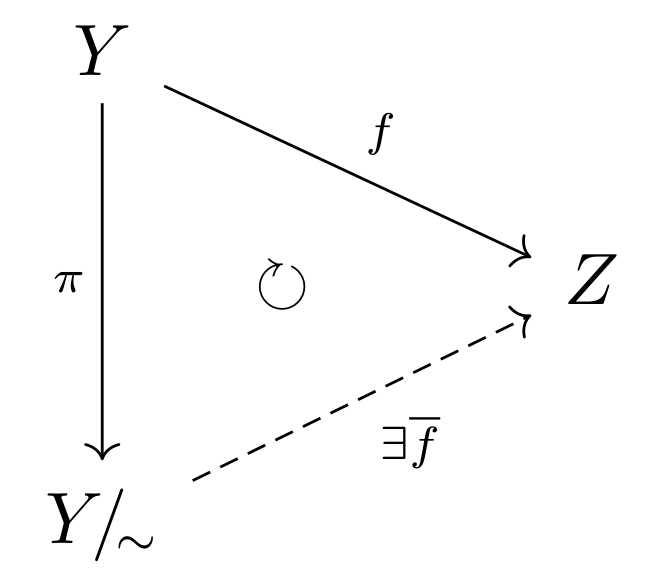
상위상과 붙이기
- 상위상을 생각하는 이유는 도형들을 적절하게 붙이는 수학적인 방법을 기술하는 것이라 할 수 있다. 앞서 서로소인 두 위상공간 $(Y_1, \mathscr{T}_1), (Y_2, \mathscr{T}_2)$에 대하여 $Y_1\amalg Y_2$ 위의 위상 $\mathscr{T}_1\amalg\mathscr{T}_2$를 자연스럽게 생각할 수 있다는 것을 언급한 바 있다. 여기서는 한 발 더 나아가 두 공간을 붙여서 만드는 새로운 위상공간을 생각하는 방법을 알아보자.
- 두 위상공간 $Y_1, Y_2$가 있고 $Y_1$의 열린집합 $U_1$, $Y_2$의 열린집합 $U_2$가 있다고 하자. 그리고 $U_1$에서 $U_2$로 가는 homeomorphism $\vartheta : U_1\to U_2$가 있다고 하자. 이 $\vartheta$를 이용해서 $Y_1, Y_2$를 서로 붙이는 것을 생각할 수 있다. 즉 $U_1$과 $U_2$를 동일시하여 $Y_1, Y_2$를 붙이는 것을 생각할 수 있다. $Y_i$들을 임의의 위상공간들로 잡았지만 처음부터 (집합적으로) 서로소인 공간들이라 생각하자.
이제 집합 $Y_1\amalg Y_2$ 위에 동치관계 $\sim$를- $\forall y_i \in Y_i,\ y_i\sim y_i$
- $\forall y_1\in U_1,\ y_1\sim\vartheta(y_1)$ 으로 정의하면 $\sim$는 잘 정의된 $Y_1\amalg Y_2$ 위의 동치관계가 된다. (이것을 확인하는 것은 당연해보이기도 하고 \[ x\sim y\quad\Leftrightarrow\quad [ (x=y) \vee\ (\vartheta(x)=y) \vee\ (\vartheta(y)=x) ] \] 인 것으로부터로도 쉽게 알 수 있다.)
이 동치관계 $\sim$로부터 만든 상위상공간 $Y=Y_1\amalg Y_2\!/\!_\sim$가 바로 위상동형사상 $\vartheta$를 이용하여 $Y_1$과 $Y_2$을 붙인(patch or glue, or clutch) 공간이다. 이 정의를 생각하면, 두 원판의 가장자리를 붙여 구면을 만드는 것을 수학적으로 잘 기술할 수 있음을 알 수 있다. - 지금 증명하고자 하는 것은 $Y_1$과 $Y_2$가 서로소인 위상공간이고 $Y_1$의 부분집합 $U_1$와 $Y_2$의 부분집합 $U_2$가 모두 열린집합(혹은 모두 닫힌집합)이고 homeomorphism $\vartheta : U_1\to U_2$가 있을 때, 각 $Y_i$에서 위와 같이 정의한 상공간 $Y$으로 가는 자연스러운 homeomorphism이 존재함을 보이고자 하는 것이다.
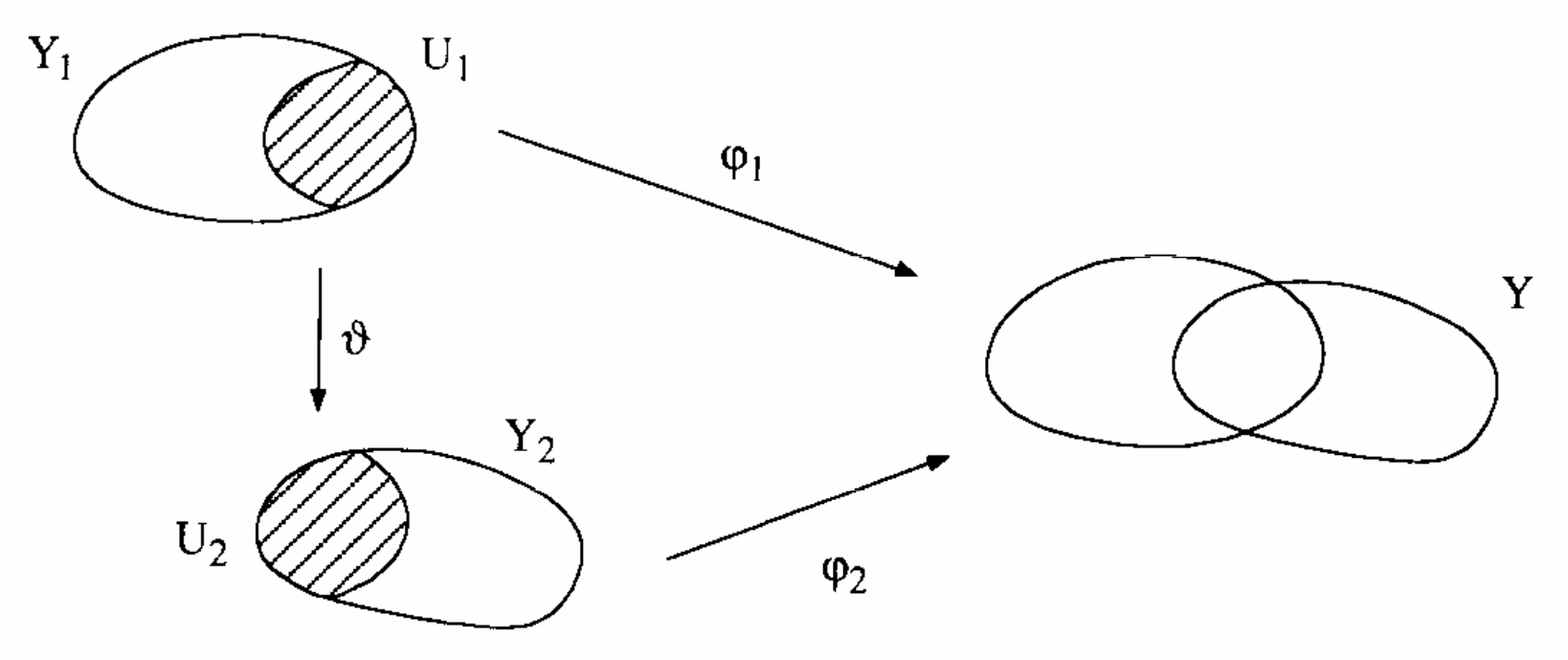
그림출처: W. Fulton의 Algebraic Topology(Springer)
Theorem 3.4 $Y_1$과 $Y_2$가 서로소인 위상공간이고 $U_1$과 $U_2$는 각각 $Y_1$과 $Y_2$의 열린집합이라고 하자. 또한 위상동형사상 $\vartheta : U_1\to U_2$가 주어져 있다고 하자. $\vartheta$를 이용하여 $Y_1, Y_2$를 붙인 상공간 $Y=Y_1\amalg Y_2$의 quotient map $\pi : Y_1\amalg Y_2\to Y_1\amalg Y_2\!/\!_\sim$으로 새로운 함수 $\varphi_i(y)$를 \[ \forall y_i\in Y_i,\quad \varphi_i(y)=\pi(y) \] 와 같이 정의하면 $\varphi_i : Y_i \to \pi(Y_i)$는 homeomorphism이다.
Proof.
편의상 $\varphi_1$가 homeomorphism인 것만 보이자. ($\varphi_2$의 경우는 완전히 동일한 방법으로 증명할 수 있다.) 우선 $\varphi_1$가 전단사임은 동치관계 $\sim$의 정의를 생각해볼 때 아주 자명하자. 또한 $\varphi_1$는 연속함수인 $\pi$의 정의역을 제한한 후 공역을 치역의 범위로 제한한 것이므로 연속함수인 것도 자명하다. 따라서 $\varphi_1$가 open map인 것만 보이면 증명이 끝난다.
이제 $V$가 $Y_1$의 임의의 열린집합이라고 하자. 보여야 할 것은 $\varphi_1(V)$가 $\pi(Y_1)$에서 open인 것이다. 이를 위해 $\pi^{-1}(\varphi_1(V))$가 open in $Y_1\amalg Y_2$임을 보이면 충분하다. 그런데 집합론의 이론을 통해
\[
\pi^{-1}(\varphi_1(V))=V\cup \vartheta(V\cap U_1)
\]
이 성립함을 쉽게 확인할 수 있다. 그런데 $\vartheta(V\cap U_1)$은 $U_2$에서 open인 집합으로 (subspace topology의 정의에 의해) $Y_2$에서 open인 적당한 집합과 $U_2$와의 교집합으로 나타낼 수 있다. 그런데 $U_2$가 $Y_2$에서 open이므로 결국 $\vartheta(V\cap U_1)$은 $Y_2$에서 open임을 알 수 있다. 따라서 $V\cup \vartheta(V\cap U_1)$은 $Y_1$에서 open인 집합과 $Y_2$에서 open인 집합의 합집합으로 $Y_1\amalg Y_2$에서 open인 집합이다.
Remark. 위의 정리 3.4에서 $U_1$과 $U_2$가 모두 open이라는 조건을 모두 closed라는 조건으로 바꾸어도 동일한 결과를 얻을 수 있다. 물론 증명도 $\varphi$가 open map임을 보이는 것 대신에 closed map임을 보이는 것으로 금방 얻을 수 있다.
- 상위상의 개념을 응용한 것의 예로 단위원판 두 개를 붙여 구면을 얻는 것을 생각해보자. $Y_1, Y_2$가 모두 단위원판이고 $U_1$과 $U_2$는 각각 $Y_1$과 $Y_2$의 경계라 하자. $Y_1\amalg Y_2$에서 $S^2$로의 함수 $f$가 $Y_1$은 $S^2$의 북반구로, $Y_2$는 $S^2$의 남반구로 보내는 전사 연속함수라 하자. 이때 $x\sim y\ \Leftrightarrow\ f(x)=f(y)$로 정의된 동치관계 $\sim$로 만든 상공간 $Y_1\amalg Y_2\!/\!_\sim$를 생각하자. 그러면 정리 3.3으로부터 $f=\overline{f}\circ \pi$를 만족시키는 연속함수 $\overline{f} : Y_1\amalg Y_2\!/\!_\sim \to S^2$이 존재함을 알고 있다.
\(\overline{f}\)의 연속성은 정리 3.3으로부터 바로 얻는 것이고, \(\overline{f}\)가 전단사함수인 것도 자명하다. 또한 \(\overline{f}\)가 closed map인 것은, \(\overline{f}\)의 정의역이 compact인 것만 보이면 충분하다. 왜냐하면 compact 집합의 닫힌 부분집합은 compact이므로, 그 닫힌 부분집합의 연속함수에 의한 상은 compact인데 지금 공역인 \(S^{2}\)가 Hausdorff 공간이므로 \(S^{2}\)의 compact subset은 닫힌 부분집합이기 때문이다. 그런데 $\overline{f}$의 정의역인 \(Y_{1}\amalg Y_{2}\!/\!_{\sim}\)은 compact 집합 \(Y_{1}\amalg Y_{2}\) 위에서 정의된 전사연속함수 \(\pi\)의 image이므로 compact이다. 따라서 \(\overline{f}\)는 homeomorphism이다.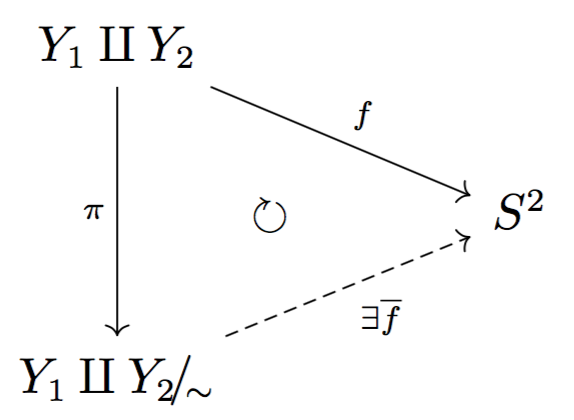
- 이제 위상공간 두 개를 붙이는 것을 일반화하여 \(\mathscr{A}\)가 임의의 index set일 때, 위상공간 \((Y_{\alpha}, \mathscr{T}_{\alpha}),\ \alpha\in\mathscr{A}\)들을 붙이는 것을 생각해보자. (물론 모든 \(Y_{\alpha}\)들이 쌍마다 disjoint하다고 가정하자.)\par
각 \(\alpha, \beta\in \mathscr{A}\)에 대하여 \(Y_{\alpha}\)의 열린집합 \(U_{\alpha\beta}\)와 homeomorphism
\[
\vartheta_{\beta\alpha}: U_{\alpha\beta}\to U_{\beta\alpha}
\]
가 있다고 하자. 그리고 이들이 조건
- \(U_{\alpha\alpha}=Y_{\alpha}\)이고 \(\vartheta_{\alpha\alpha}\)는 \(Y_{\alpha}\) 위의 항등사상이다.
- 임의의 \(\alpha, \beta, \gamma\in\mathscr{A}\)에 대하여, \(\vartheta_{\beta\alpha}(U_{\alpha\beta}\cap U_{\alpha\gamma})\subset U_{\beta\gamma}\)이고 \[ \vartheta_{\gamma\alpha}=\vartheta_{\gamma\beta}\circ\vartheta_{\beta\alpha}\quad\mbox{on}\quad U_{\alpha\beta}\cap U_{\alpha\gamma} \] 이다.
Lemma 3.5
- 각 \(\varphi_{\alpha}(Y_{\alpha})\)는 \(Y\)의 열린집합이다.
- \(\varphi_{\alpha}\)는 embedding map, 즉 \(\varphi_{\alpha}\)는 \(Y_{\alpha}\)에서 \(\varphi_{\alpha}(Y_{\alpha})\) 위로 가는 homeomorphism이다.
- \(Y=\bigcup_{\alpha\in\mathscr{A}}\varphi_{\alpha}(Y_{\alpha})\)
- \(\varphi_{\alpha}(U_{\alpha\beta})=\varphi_{\beta}(U_{\beta\alpha})\)
- \(U_{\alpha\beta}\) 위에서 \(\varphi_{\beta\alpha}=\varphi_{\beta}^{-1}\circ\varphi_{\alpha}\)
Proof. 이것의 증명은 복잡하지 않다. 추후에 복습할 시간이 또 있다면 그때 다시 써보자.
- 위의 논의가 각 \(U_{\alpha\beta}\)들이 모두 \(Y_{\alpha}\)의 닫힌집합일 때에도 가능함을 확인해보자.